Delta Theta Ratio – What Is The Ideal Ratio?

by Gavin in Blog

May 6, 2022 • 4 comments

The non-directional trader wants to hedge delta to make it delta-neutral and have theta as large as possible. In theory, they want the delta theta ratio to be zero. In practice, this is not achievable because delta changes continuously as the price of the underlying moves. And you don’t want to be constantly over-adjusting your positions.

Contents

• Delta Theta Ratio
• Bull Put Spread
• If Closer To The Money
• If At Lower Volatility
• Iron Condor
• Iron Butterfly
• Broken Wing Butterfly
• If Closer To Expiration
• FAQ

Delta Theta Ratio

So what is the ideal delta theta ratio in practice?

Tom Sosnoff of TastyTrade was asked a similar question at a symposium when he answered:

“A lot of this depends on where the markets are based on current levels of implied volatility.”

At the time that he gave his answer, the market volatility was low, which means lower theta, and higher delta-theta ratios. He continues:

“Our deltas are much higher than our thetas right now. Because I don’t feel the risk in short premium is worth the reward because volatility is so low. So our deltas are 2 or 3 X our theta right now. That’s not a perfect world. That’s exactly what you don’t want. … In a perfect world, you would much prefer your deltas about half of your theta.” source: YouTube

Basically, for a non-directional trader capitalizing on theta decay, you want to try to target a 0.5 delta-to-theta ratio. Keep delta at 50% or less of your theta, and you should be good.

This ratio may not always be possible when the price moves all around in the middle of a trade. It also depends on the underlying. It is more achievable in the indices such as RUT (Russell 2000) and SPX (S&P 500).

That’s one of the reasons why many non-directional traders like working with the indices. Another reason is that it avoids large moves of individual stocks that may be experiencing a catalyst event.

Let’s look at the starting delta-theta ratios of some option strategies.

Bull Put Spread

Here is a bull put spread on RUT with 29 days to expiration:

Date: March 16, 2022

Price: RUT @ $2013

Buy two April 14 RUT 1835 puts
Sell two April 14 RUT 1840 puts

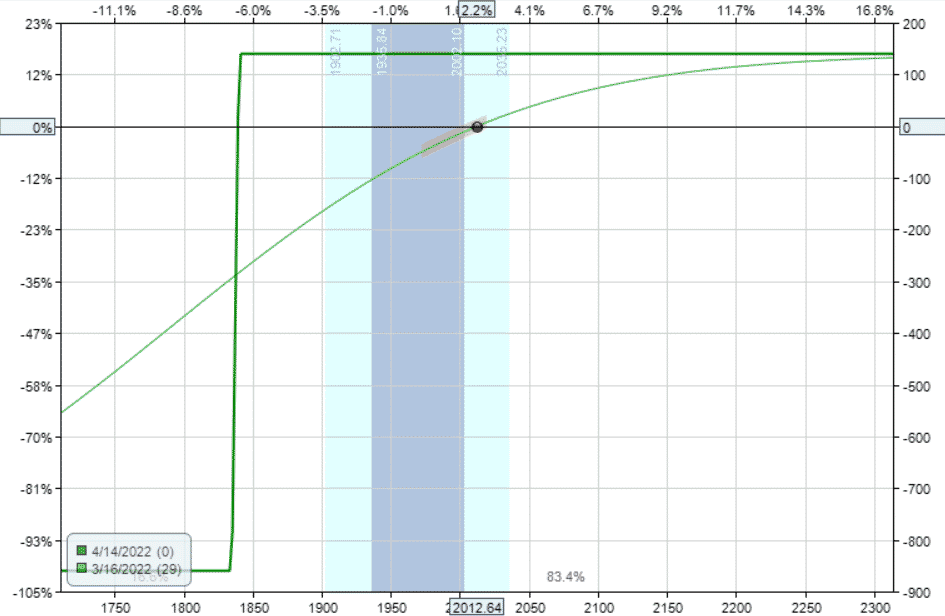
source: OptionNet Explorer

Delta: 1.12

Theta: 2.59

Vega: -5.86

Gamma: -0.01

The delta/theta ratio is 1.12/2.59 = 0.4

Note that we are selling two contracts. If we were selling one contract, all the Greeks would be halved, but the ratio remains at 40%.

The short strike in this example was at 18-delta.

If Closer To The Money

If we moved the short strike closer to the money at the 30-delta, we would get a delta theta ratio of 1.74/1.68 = 1.0.

The trade becomes more directional. As we go closer to the money, the Delta (and Vega) becomes more dominant in relation to Theta.

If At Lower Volatility

VIX at the time on March 16 was moderately high at 29. A more appropriate volatility metric is the RVX (CBOE Ruessel 2000 Volatility Index), which at the time is at 33.

If we had put on a similar trade in a low volatility environment such as Janurary 4th, 2022.

Buy two February 4 RUT 2110 put
Sell two February 4 RUT 2115 put

The Greeks would be different:

Delta: 1.25

Theta: 2.11

Vega: -7.78

Gamma: -0.01

And the delta/theta ratio would be higher at 0.6, or 60%.

Iron Condor

Keeping with the March 16 bull put spread with the short strike at 18-delta, we now add a bear call spread to make an iron condor:

Date: March 16, 2022 Price: RUT @ $2013

Buy two April 14 RUT 1835 puts
Sell two April 14 RUT 1840 puts
Sell two April 14 RUT 2220 calls
Buy two April 14 RUT 2225 calls

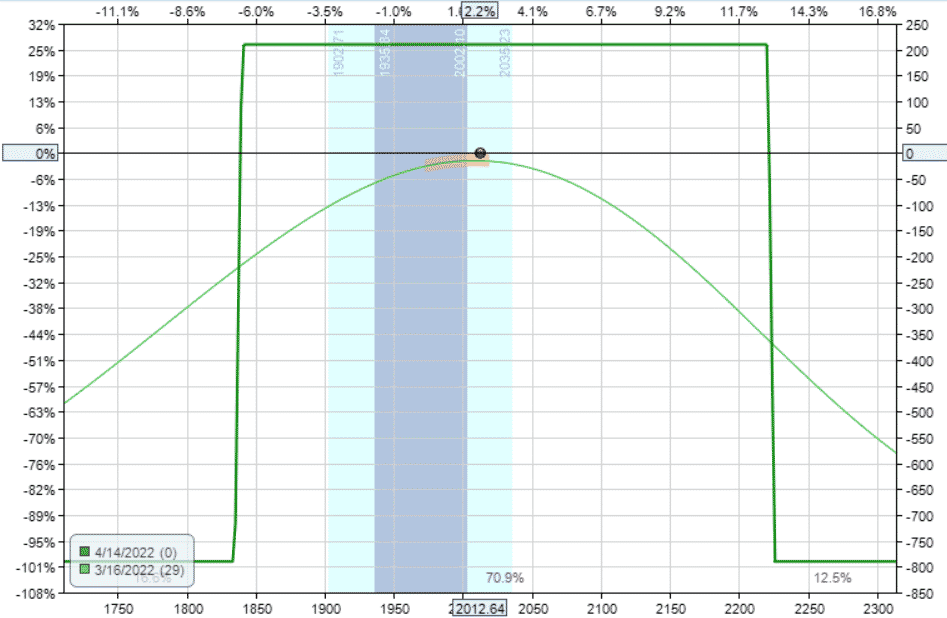
Delta: -0.04

Theta: 6.87

Vega: -15.42

Gamma: 0.00

We kept the width of the bear call spread to be the same as the bull put spread, but we positioned it further away from the money such that the resulting delta is near zero.

Because we have eliminated delta, the delta theta ratio here is 0.01 — just about perfect.

As it is, the short-strike of the bear call spread is at 8-delta and 207 points away from the current price. This is quite a bit further away from price that the bull put spread whose short-strike is only 173 points away.

If we had positioned the bear call spread equidistance away with short-strike at 2185, its delta would be -0.47 and theta would be 7.6, resulting in a higher delta-theta ratio of 0.06 — still very good, but not as perfect.

Sample Iron Condor Trading Plan

Iron Butterfly

If we move the two short strikes of the iron condor to at-the-money and widen the wings, we get an iron butterfly.

Date: March 16, 2022

Price: RUT @ $2013

Buy one April 14 RUT 1920 puts
Sell one April 14 RUT 2010 puts
Sell one April 14 RUT 2010 calls
Buy one April 14 RUT 2100 calls

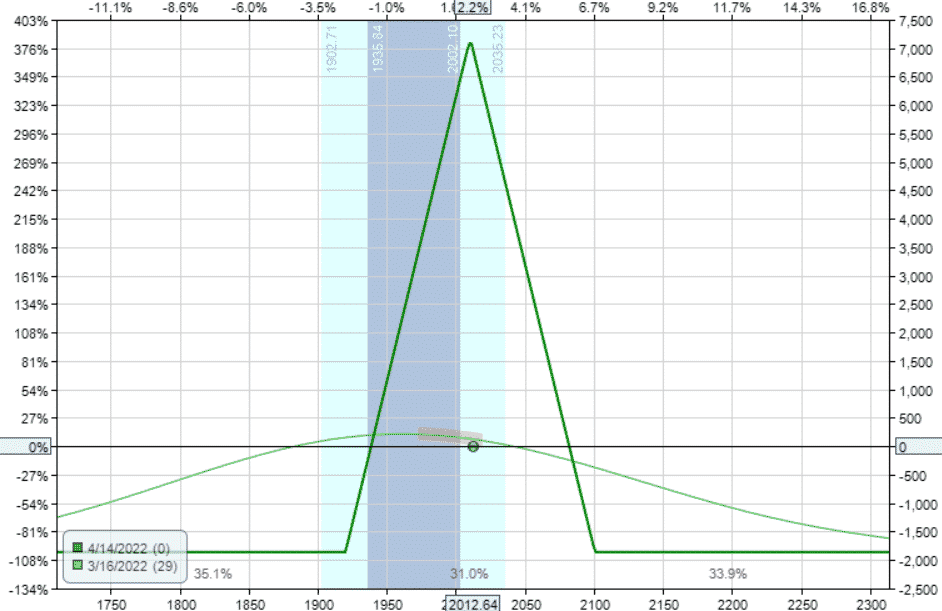
Delta: -3.52

Theta: 28.29

Vega: -59.65

Gamma: -0.04

Even after dropping down to one contract butterfly, this trade is twice as large as the iron condor. See that the max risk on this trade is $1860, whereas the condor is $790.

Even taking this into account, butterflies typically have larger theta and vega than condors because they are selling at-the-money strikes.

The delta-theta ratio here is 3.52/28.29 = 0.12

We are just using the magnitudes of delta and theta. In calculating the ratio, we are not concerned with the negative in the delta.

However, as a trader, we do need to note that this trade starts out with a negative delta which is slightly bearish. Even though this butterfly is symmetrically centered, the bearish tilt is due to the put-call skew.

Some traders may prefer this negative delta as a hedge against the negative vega in a market downturn.

But other traders may prefer to start out with a more neutral delta by adjusting the strikes widths into a broken wing butterfly as follow.

Broken Wing Butterfly

Date: March 16, 2022

Price: RUT @ $2013

Buy one April 14 RUT 1950 put
Sell one April 14 RUT 2010 put
Sell one April 14 RUT 2010 call
Buy one April 14 RUT 2065 call

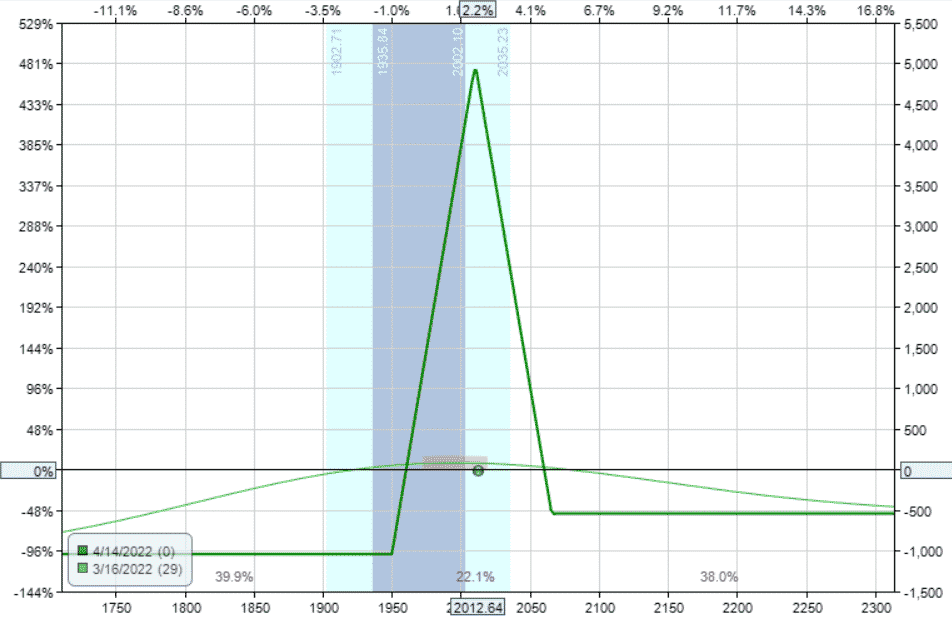
Delta: -0.44

Theta: 11.16

Vega: -25.34

Gamma: 0.01

The delta is closer to zero, and the delta-theta ratio has been reduced to 0.04.

Alternatively, some traders prefer to have the downside expiration breakeven further away from the current price. The Rhino strategy, for example, starts out with this configuration.

This can be achieved by setting the upper long leg to be near where current price is.

Buy one April 14 RUT 1900 put
Sell two April 14 RUT 1960 puts
Buy one April 14 RUT 2010 put

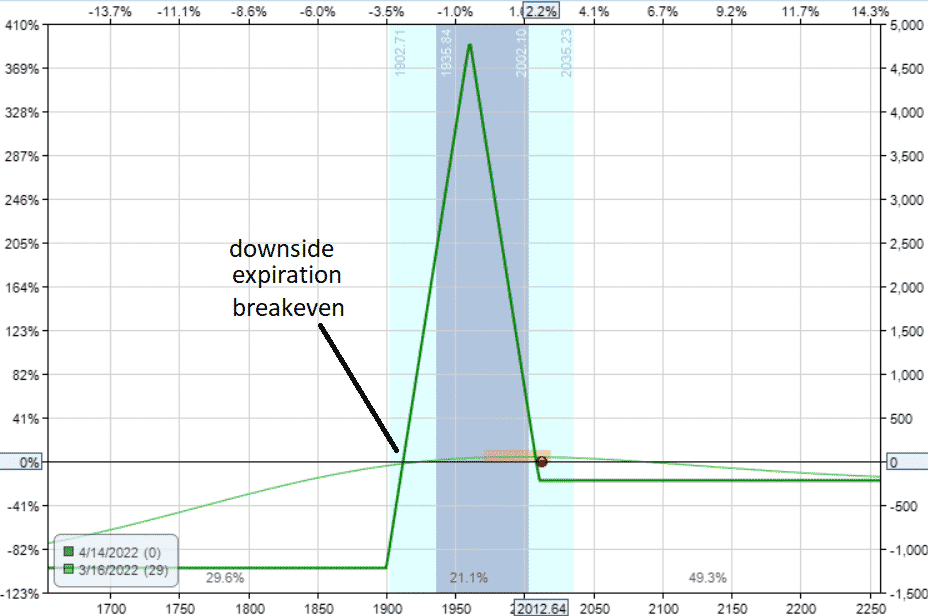
This time, we used an all-puts broken wing instead.

The Greeks and the ratios end up being quite similar:

Delta: -0.30

Theta: 9.4

Vega: -17.69

Gamma: -0.06

Delta/Theta: 0.03

If Closer To Expiration

Now suppose we have a similar broken-wing butterfly starting at 14 days to expiration instead of 29 days:

Buy one March 30 RUT 1910 put
Sell two March 30 RUT 1965 puts

Buy one March 30 RUT 2010 put

The Greeks would be as follow:

Delta: -0.80

Theta: 21.18

Vega: -17.50

Gamma: -0.08

Delta/Theta: 0.04

Theta has increased for sure. In fact, it has grown bigger than vega. (This means shorter-term trades have less risk due to changes in volatility than longer-term trades.)

Another Greek that has grown is Gamma.

Gamma is the rate of change of Delta. A larger Gamma means that Delta will fluctuate more, causing more rapid changes in the Delta/Theta ratio.

If you were to follow my advice in Bootcamp Day 1.

For a typical Iron Condor that began with a Delta / Theta Ratio near 0%, you want to adjust when the Delta / Theta Ratio gets to around 30%.

Then you need to monitor the trade more frequently and make adjustments more frequently as this ratio gets out of line at an increasing rate.

If you’ve enjoyed all this talk about Greek ratios, visit the topic of Theta-Vega ratios.

FAQ

What Is The Delta Theta Ratio?

The Delta Theta Ratio is a metric used to assess the balance of risk and reward in an options trading portfolio.

It compares the rate of change of an options position’s delta to the rate of change of its theta, providing an indication of how much potential profit or loss the position may experience for each day that passes.

How Is The Delta Theta Ratio Calculated?

The Delta Theta Ratio is calculated by dividing the absolute value of the position’s delta by the position’s theta.

This provides a ratio that represents the potential profit or loss that the position may experience for each day that passes.

How Can I Use The Delta Theta Ratio To Manage My Portfolio?

The Delta Theta Ratio can be used to manage your options trading portfolio by helping you balance risk and reward.

A high ratio indicates that the position is more sensitive to changes in the underlying asset’s price, while a low ratio indicates that the position is more sensitive to changes in time decay.

Traders can use this information to adjust their portfolio to achieve their desired risk-reward profile.

What Are The Limitations Of Using The Delta Theta Ratio?

The Delta Theta Ratio is just one tool among many that traders can use to manage their options trading portfolios.

It is important to remember that it is based on estimates and assumptions about future market conditions, and actual market conditions may differ.

Additionally, the Delta Theta Ratio may not be appropriate for all traders or trading strategies.

Where Can I Learn More About The Delta Theta Ratio?

There are many resources available to help traders learn more about the Delta Theta Ratio, including online courses, trading books, and forums or discussion groups. It’s important to carefully research and evaluate any educational resources before investing time or money in them.

Trade safe!

Disclaimer: The information above is for educational purposes only and should not be treated as investment advice. The strategy presented would not be suitable for investors who are not familiar with exchange traded options. Any readers interested in this strategy should do their own research and seek advice from a licensed financial adviser.