

Today, we are looking at theta decay and specifically which option strategy has the most time decay.
Read on to find out.
Contents
- Introduction
- Non-directional Undefined-Risk Strategies
- Non-Directional Two-Legged Defined-Risk Strategy
- Non-Directional Three-Legged Defined-Risk Strategy
- Non-Directional Four-Legged Defined-Risk Strategies
- Summary
Introduction
Non-directional options investors like to generate income via “time decay“.
This type of trade typically (but not always) involves selling an option spread and then watching the value of the option spread decay with time.
The goal is to buy it back at a lower price to exit with a profit.
We want to answer today which of the following non-directional options strategies has the most time decay.
Like the Oscars Academy Awards that judge winners based on the film genre, we need to judge the option strategies based on the type of strategy.
It wouldn’t be fair to compare the time decay of a two-legged undefined-risk strategy with a four-legged defined-risk strategy, would it?
Non-Directional Undefined-Risk Strategies
The winner of best time decay in the non-directional undefined-risk category is: (drum roll please)
The Short Straddle
Date: Aug 6, 2021
Sell one Sep 17, 2021 SPY $442 call @ $7.68
Sell one Sep 17, 2021 SPY $442 put @ $7.87
Credit: $1554.50
Margin: $8,850
Theta: 19.53
Theta/Margin: 0.22%
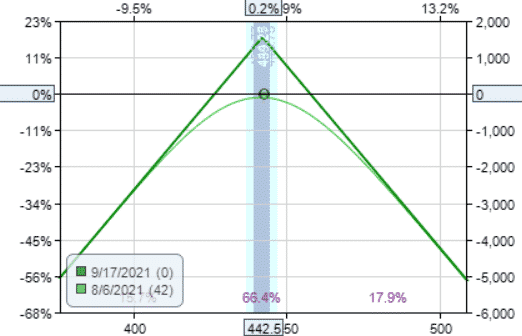
It narrowly beats out its competitor, the short strangle.
The Short Strangle
Date: Aug 6, 2021
Sell one Sep 17, 2021 SPY $455 call @ $1.73
Sell one Sep 17, 2021 SPY $426 put @ $4.11
Credit: $584
Margin: $7600
Theta: 15.86
Theta/Margin: 0.21%
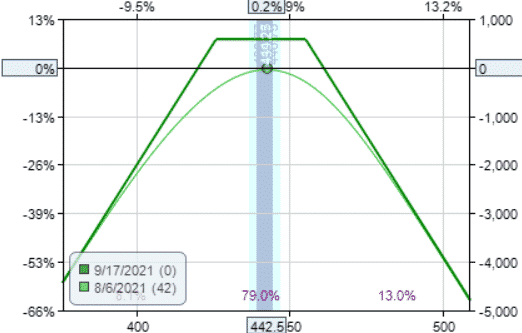
This is because the straddle sells the at-the-money (ATM) strikes which have the greatest extrinsic value.
The extrinsic value of an option is the portion of the option that decays.
The strangle sells out-of-the-money options.
The further out of the money, the less time decay.
In our example, the strangle was sold at the 25-delta.
Non-Directional Two-Legged Defined-Risk Strategy
The winner in this category is the calendar.
It won by default since there were no other nominees in this category.
Calendar
Date: Aug 6, 2021
Sell one Sep 17 SPY $442 put @ $7.87
Buy one Oct 15 SPY $442 put @ $11.21
Debit: $334
Margin: $334
Theta: 1.57
Theta/Margin: 0.47%
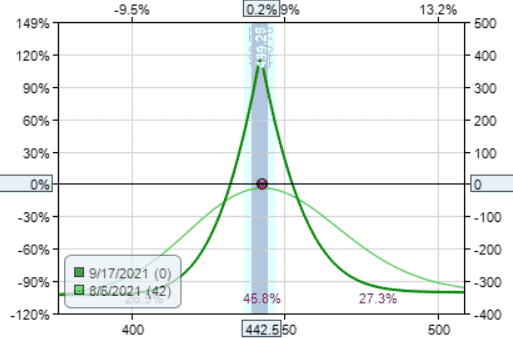
We increase the theta decay by moving the long leg further out in time, but this also increases the margin used.
For example,
Date: Aug 6, 2021
Sell one Sep 17 SPY $442 put @ $7.87
Buy one Jan 21 SPY $442 put @ $20.09
Debit: $1222
Margin: $1222
Theta: 3.74
Theta/Margin: 0.31%
The net result is a decrease in “theta efficiency” from 0.47% to 0.31%.
Theta efficiency is the amount of theta achieved relative to the amount of margin used.
The ATM call calendar will be within the same ballpark as the ATM put calendar — as we can see here:
Date: Aug 6, 2021
Sell one Sep 17 SPY $442 call @ $7.68
Buy one Jan 21 SPY $442 call @ $18.60
Debit: $1092
Margin: $1092
Theta: 3.74
Theta/Margin: 0.34%
Non-Directional Three-Legged Defined-Risk Strategy
Diagonalized Collar
Non-directional strategies typically only consist of strategies with an even number of option legs.
However, using creativity, one might come up with a three-legged construction like this (if you consider the long stock a “leg”).
Date: Aug 6, 2021
Buy 100 share of SPY @ $442.5
Buy one Jan 21, 2022 SPY $442 put @ $20.09
Sell one Sep 1, 2021 SPY $442 call @ $7.68
Debit: $45,491
Margin: $23,366
Theta: 4.05
Theta/Margin: 0.02%
The graph looks pretty non-directional to me.
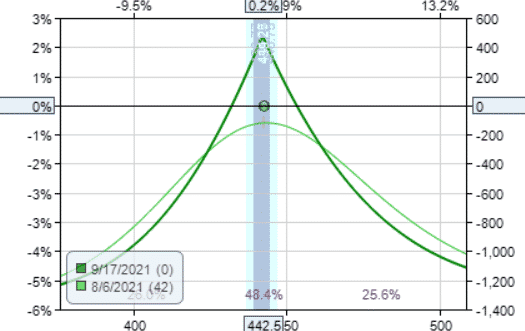
Because this “diagonalized collar” utilizes long stock, it is not very capital efficient, resulting in a low theta/margin ratio.
Non-Directional Four-Legged Defined-Risk Strategies
We have lots of candidates in this category.
Butterfly
The iron butterfly is the defined-risk version of the straddle.
Date: Aug 6, 2021
Buy one Sep 17 SPY $455 call @ $1.73
Sell one Sep 17 SPY $442 call @ $7.68
Sell one Sep 17 SPY $442 put @ $7.87
Buy one Sep 17 SPY $429 put @ $4.59
Credit: $922.50
Margin: $377.50
Theta: 3.40
Theta/Margin: 0.90%
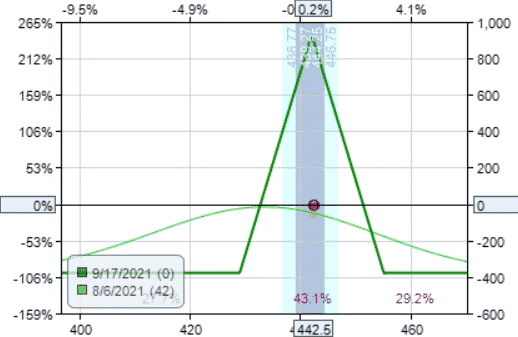
It has a very low margin, which gives it excellent theta efficiency.
Iron Condor
The iron condor is the defined-risk version of the strangle.
Date: Aug 6, 2021
Buy one Sep 17 SPY $465 call @ $0.40
Sell one Sep 17 SPY $455 call @ $1.73
Sell one Sep 17 SPY $426 put @ $4.11
Buy one Sep 17 SPY $416 put @ $2.90
Credit: $254.50
Margin: $745.50
Theta: 5.12
Theta/Margin: 0.69%
In both the iron condor and iron butterfly, the theta is increased when we increase the width of the strikes in the wings.
If we widen the wings on the condor to match the wing size of the iron butterfly, then we have
Date: Aug 6, 2021
Buy one Sep 17 SPY $468 call @ $0.26
Sell one Sep 17 SPY $455 call @ $1.73
Sell one Sep 17 SPY $426 put @ $4.11
Buy one Sep 17 SPY $413 put @ $2.62
Credit: $297
Margin: $1003
Theta: 6.39
Theta/Margin: 0.64%
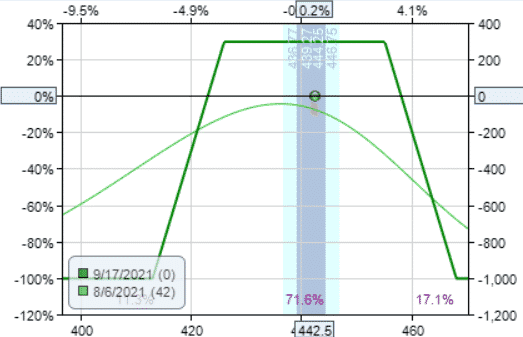
The thetas are close.
But the butterfly has better theta efficiency.
Double diagonal
The double diagonal is like the iron condor, except that the long strike is moved out to a later expiration
Date: Aug 6, 2021
Buy one Oct 15 SPY $468 call @ $1.14
Sell one Sep 17 SPY $455 call @ $1.73
Sell one Sep 17 SPY $426 put @ $4.11
Buy one Oct 15 SPY $413 put @ $4.98
Debit: $27.50
Margin: $1327.50
Theta: 4.85
Theta/Margin: 0.37%
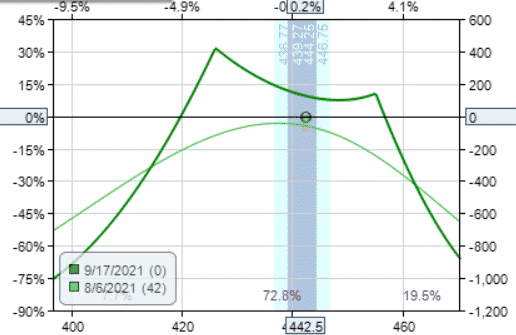
Here, the double diagonal incurs a slight debit.
But sometimes it can end giving a slight initial credit, as we see next when we move the two diagonals so that both short strikes are at the money (while maintaining the same wing width)
At-the-money double diagonal
Date: Aug 6, 2021
Buy one Oct 15 SPY $455 call @ $4.00
Sell one Sep 17 SPY $442 call @ $7.68
Sell one Sep 17 SPY $442 put @ $7.87
Buy one Oct 15 SPY $431 put @ $8.04
Credit: $351
Margin: $949
Theta: 4.62
Theta/Margin: 0.49%
The graph looks more like a straddle…
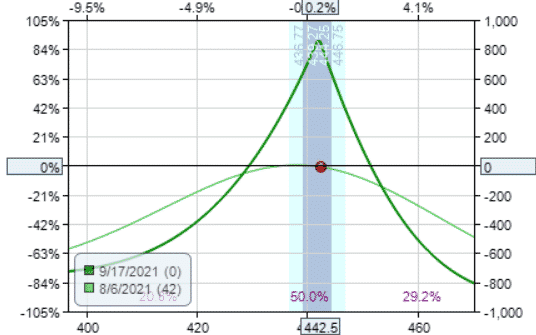
Double calendar
The double calendar is like the double diagonal, except the long strike is the same as the short strike.
Date: Aug 6, 2021
Buy one Oct 15 SPY $455 call @ $4.00
Sell one Sep 17 SPY $455 call @ $1.73
Sell one Sep 17 SPY $426 put @ $4.11
Buy one Oct 15 SPY $426 put @ $7.00
Debit: $516
Margin: $516
Theta: 1.07
Theta/Margin: 0.21%
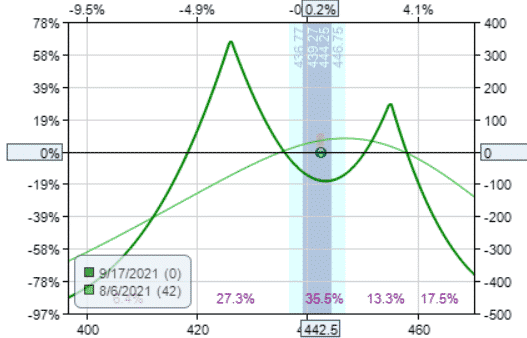
The double calendar has less theta decay than the double diagonal.
These graphs are off-centered or not quite symmetrical because of the put/call skew, especially in a market ETF like the SPY.
The puts are selling at a greater premium than the calls of the same delta.
Summary
Now we understand what parameters to tweak to achieve good theta decay.
- Sell at the money
- Buy further out in time
- Buy further away from the money
In terms of absolute theta achieved, the short straddle is the winner with the greatest time decay.
It is followed by the second runner-up, the short strangle.
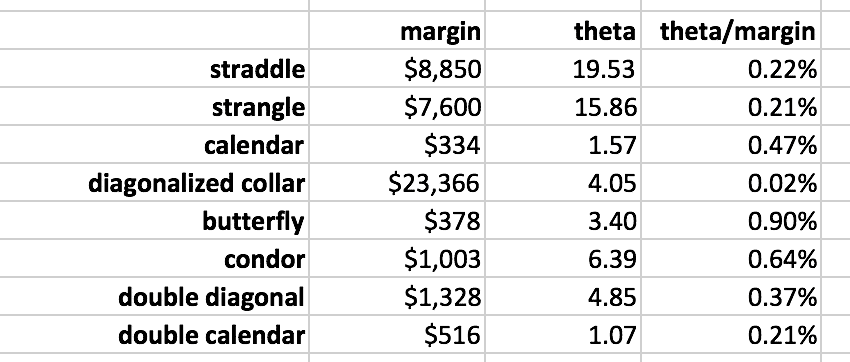
By defining the risk, we reduced the margin requirements and increased the theta efficiency (the theta per margin used). We can see this with the butterfly, condor, calendars, and diagonals.
Keep in mind that these theta values are only at the start of the trade.
Like all Greeks, it changes dynamically as the trade progress due to changes in price, volatility, and the passage of time.
Also, there are other factors that contribute to the selection of option strategies besides theta.
Condors are best traded when implied volatility is high. And calendars are best traded when implied volatility are low.
When selling options near the money, be aware of assignment risk, especially when close to expiration.
Some investors may wish to trade on the SPX cash-settled index instead of the SPY ETF to avoid this.
Trade safe!
Disclaimer: The information above is for educational purposes only and should not be treated as investment advice. The strategy presented would not be suitable for investors who are not familiar with exchange traded options. Any readers interested in this strategy should do their own research and seek advice from a licensed financial adviser.










