

Interest rates do affect option pricing – albeit with a very small effect.
According to the Black-Scholes pricing model, the value of an option depends on five factors:
- The stock price (or the underlying price)
- The strike price
- The volatility
- The time remaining in the option
- The risk-free interest rate
In this article, we will focus on the effect of interest rates on options.
While it is the least important of the five factors, it is worth discussing because it is one of the inputs into the infamous Black-Scholes model.
Intuitively, the interest rate should affect an options price.
Buyers of an option are investing.
Like any investment, the investors have an “opportunity cost” to consider.
If they invest money into options contracts, they cannot use the money elsewhere, such as investing in U.S. Treasury bills, which effectively return a risk-free interest rate.
Therefore, investors will only invest money into options contracts if they think they can get a better return on the options than the risk-free interest rate.
Whether the risk-free interest rate is high or low will affect the buyer’s decision, which in turn will affect the demand for the options and the price of the options.
Contents
How Much Will the Interest Rate Affect The Price Of An Option?
The option Greeks are what tell you how much an option’s price is affected by changes in any of the Black Scholes inputs.
Let’s start with something that’s more familiar – delta.
Delta is the option Greek that relates the change in the underlying price to the change in the option’s value.
Vega is the option Greek that relates the change in the volatility to the change in the option’s value.
Theta is the option Greek that relates the change in the remaining time of the option to the change in the option’s value.
And finally, Rho is the option Greek that relates the change in the interest rates to the change in the option’s value.
Delta, Vega, Theta, and Rho are the first-order Greeks.
They are related to the change in each of the inputs to the Black-Scholes.
There is no Greek for the change in the strike price because the strike price of an option does not change.
Gamma is not a first-order Greek. It is a second-order Greek that relates the change of delta with respect to the change in the underlying price.
For the most part, the first-order Greeks are more important to an option’s price than the second-order Greeks, except for Rho and Gamma.
Most investors rightfully consider gamma to be more important than Rho.
Rho is the least important of the first-order Greeks.
And gamma is the most important of the second-order Greeks.
In many options analytics software, you will see gamma values but not Rho.
This shows the relative importance of the two Greeks.
Definition Of Rho
The number given by Rho is the change in an option’s price for a one percent change in the risk-free interest rate (often referenced as the U.S. treasury bill rate).
The Rho of call options is positive.
This means that if the interest rates increase, the value of a call option increases, assuming all other factors remain the same.
Let’s say that an investor wants to borrow some money to put into either stock shares or options contracts.
If interest rates are high, it would cost them more to borrow.
The “cost of carrying” is high.
Hence they would rather borrow less and invest in long call options instead of long stock since options have leverage making them cost less to control an equivalent number of shares of stock.
The greater demand for call options increases the call prices as interest rates increase.
This is why Rho is positive for call options.
The Rho of put options is negative.
This means that if the interest rates increase, the price of a put option decreases.
And if interest rates decrease, the value of put options increases.
Consider the case where an investor wants to short an equity.
They can either short the stock and immediately receive cash into their account.
Or they can buy put options.
When interest rates are high, they are likely to do the former because the credit they receive can be placed into a risk-free interest-bearing vehicle to generate additional income.
Plus, there is less motivation to borrow money in order to buy puts.
The lower desire to buy put options decreases the value of the put options.
That is why the put options value drops as the interest rate increases.
It is important to keep in mind that these interest rate effects assume that all other effects are held constant.
In reality, all the other effects are not constant and actually have a greater influence on the option price than the interest rate effects.
Options Sensitivity To Interest Rates
Rho indicates the sensitivity of an option price to a change in interest rate.
A larger magnitude of Rho (regardless of the sign) means that the option is more sensitive to a change in the interest rate.
Out-of-the-money options are less sensitive to interest rates than at-the-money options.
Interest rates affect Longer-term options more than shorter DTE (days-to-expiration) options. This makes sense.
How much will a change in interest rate affect a zero-DTE option? Hardly at all.
Therefore, Rho is larger for longer-dated options.
Most investors will only need to worry about Rho when LEAPS options are involved.
These Long-term Equity AnticiPation Securities are options with an expiration date of more than a year.
Also significant is when the interest rate is expected to change a lot during the option’s lifetime.
Other times when interest rates may become significant to option pricing is when rates are extremely high, such as in the 1980s when interest rates were near 20%.
Example Of Interest Rate On The Price Of The Option
Mathematically speaking, the interest rate input into the Black-Scholes formula has minor effects on the final result of the price output of the formula.
Using an online Black-Scholes calculator, let’s input the values of a typical call option.
Current stock price: $88
Strike price: $90
Time to maturity: 0.08 years (about one month)
Dividend yield: 2%
Volatility 28%
Risk-free interest rate: 5%
The resulting call and put option price that the calculator gave was:
Call option price: $2.00
Put option price: $3.78
If we change the input from a 5% risk-free interest rate to 4.75%, the result shows negligible change from the original.
Call option price: $2.00
Put option price: $3.79
The option price barely changed. Is the calculator working?
If we changed the input from a 5% risk-free interest rate to 1%, the result would be:
Call option price: $1.89
Put option price: $3.96
The calculator is working.
That was a gigantic change in interest rate, yet the price change in the call and the put option was relatively minor.
Frequently Asked Questions:
Why do we have to enter dividend yield into the Black-Scholes calculator when it is not one of the inputs into the formula?
Indeed, the original Black-Scholes formula does not have dividend yield in its formula.
That is because the formula assumes that it is calculated for stocks without dividends and with European-style expiration where options cannot be exercised early.
People realized that this was a limitation of the formula because it was clear that dividends impact option pricing.
So the formula was expanded by Robert Merton to consider dividend yields.
The calculator was probably using this expanded formula.
The effects of dividends are also relatively minor in the price of an option.
How can we calculate Rho for the entire position if it consists of multiple legs?
Like any other Greek, you can calculate the combined Rho for the entire multi-leg position by summing the rho values for the individual legs, considering flipping the sign if you are selling the option instead of buying the option.
Where can I find analytical software that provides values of Rho for free?
OptionStrat has rho information for single-leg options.
You can then manually calculate it for a multi-leg position.
Or subscribe to a paid subscription, and OptionStrat will calculate the combined Greeks for you.
What is the impact of interest rates on a covered call?
A covered call consists of long stock plus selling a call option on that stock.
For example, an investor buys 100 shares of Disney (DIS) stock at $88.25 per share on May 26, 2023. He then sells one $93 call option expiring on June 30.
This position is depicted in OptionStrat with a rho of -2.29.
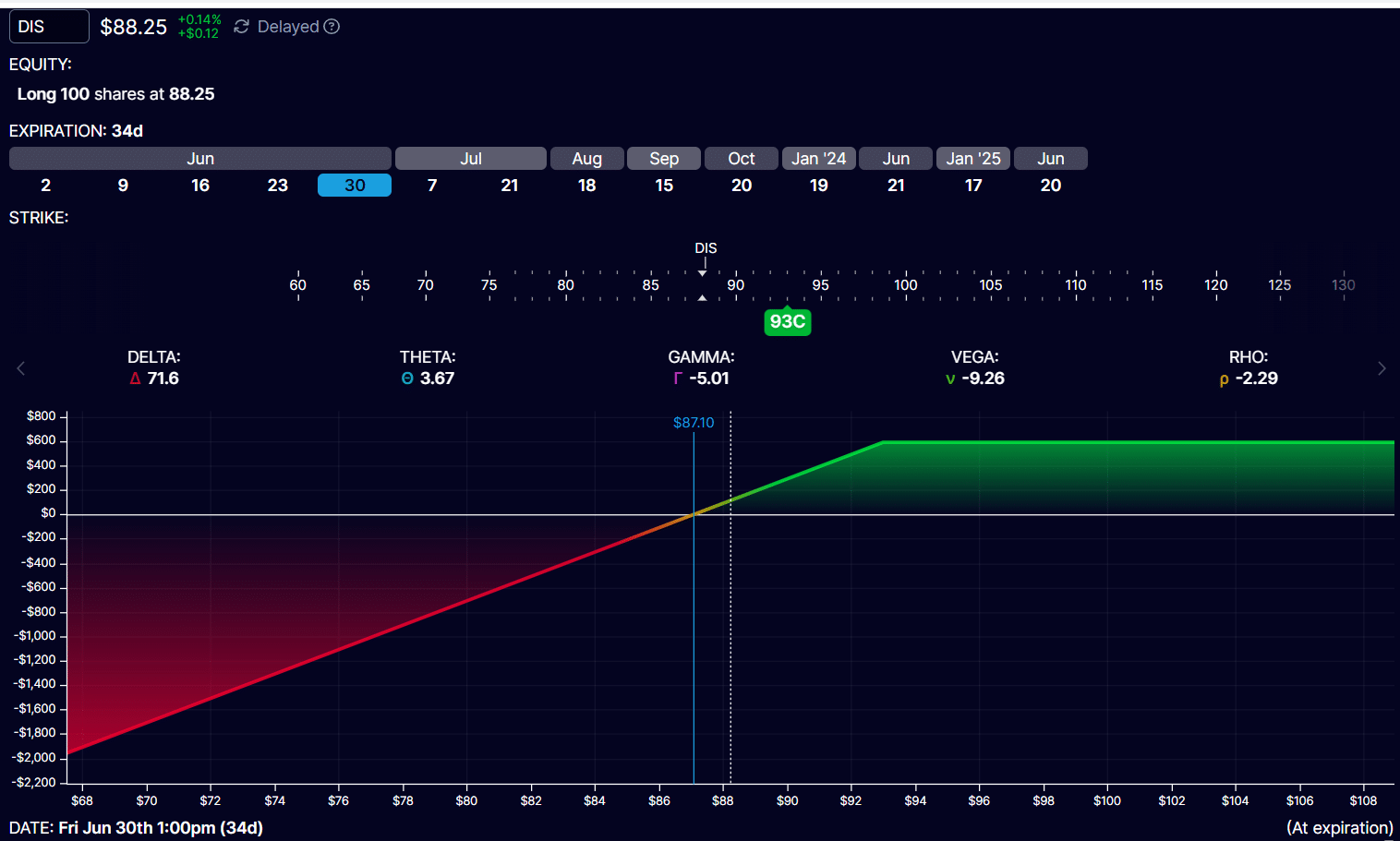
Source: OptionStrat.com
Recall that the Rho of a call option is positive.
If you look up the value of Rho for the $93 DIS call, you will find that it is 2.29.
But when you sell that option, you flip the sign.
So the Rho of the short $93 DIS call is -2.29.
The Rho of a stock is always zero because the value of the stock does not depend on the interest rate. Interest rate changes only affect the options.
When you sum all the components of the covered call position (-2.29 + 0), you arrive at a rho value of -2.29 for the covered call position.
This means that if the interest rate goes up 1%, the value of the covered call position will theoretically drop by 2.29 – assuming that all other factors did not change.
In reality, all other factors will change and will likely have a greater effect on the position than the change in interest rate.
Why would covered calls be worth less (or would be less desirable) when interest rates increase?
Covered calls are capital intensive with at least 100 shares of stock.
In our example, 100 shares are worth $8825.
An investor who does not have that much capital sitting at his disposal will need to borrow that capital at the interest rate. Investors are less inclined to perform that borrowing when the interest rate is high.
What is the impact of interest rates on a long straddle?
A long straddle consists of a long call option and a long put option on an underlying asset.
Here is a straddle on DIS with the $88 call option and $88 put option with expirations on June 30.
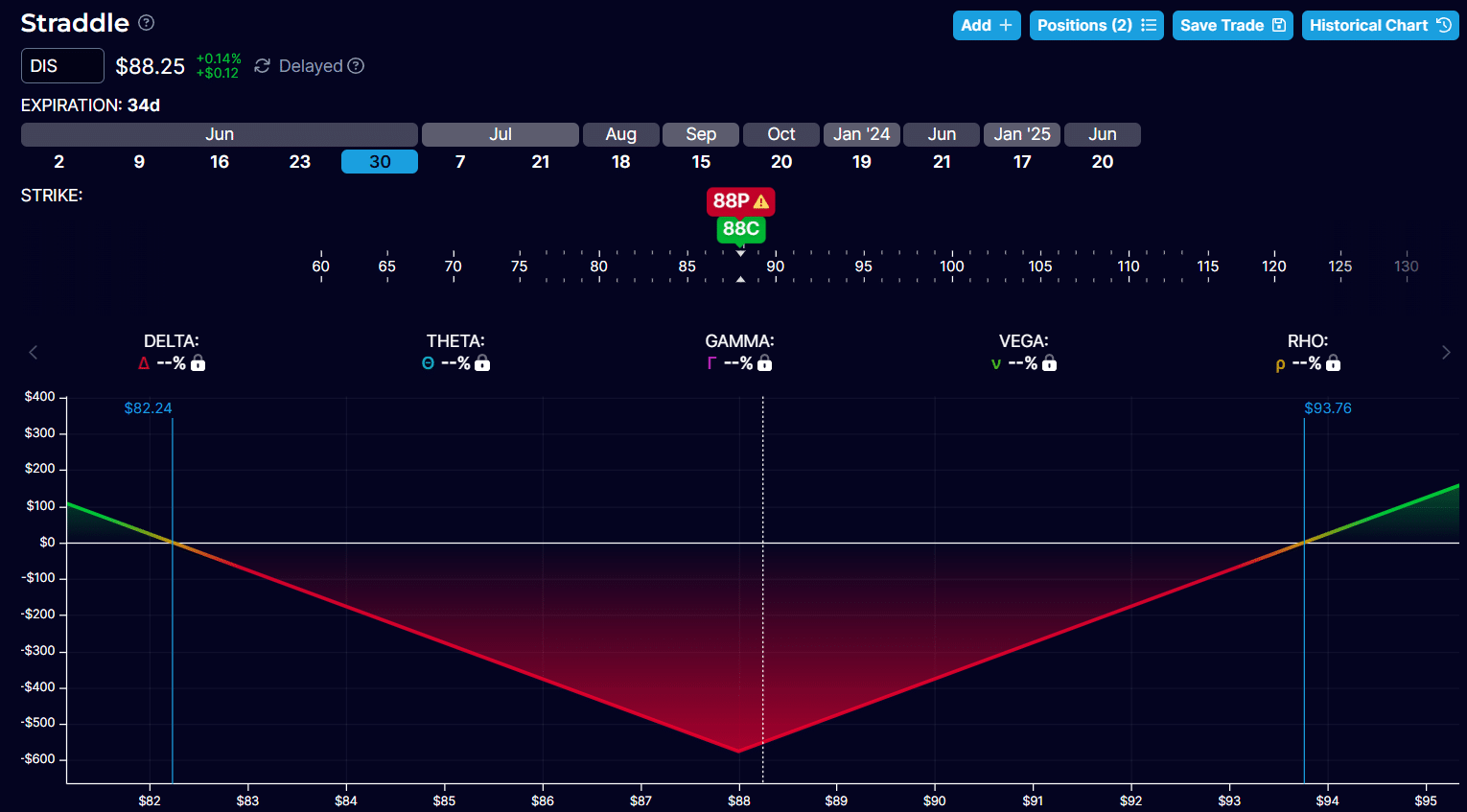
The combined Greeks of multi-leg option positions are only available in OptionStrat for paid members.
But we can compute the combined Greeks ourselves by noting the Greeks of the individual options and summing them (taking care of flipping the sign if we are selling).
The Rho of the $88 call is 0.0441 per share.
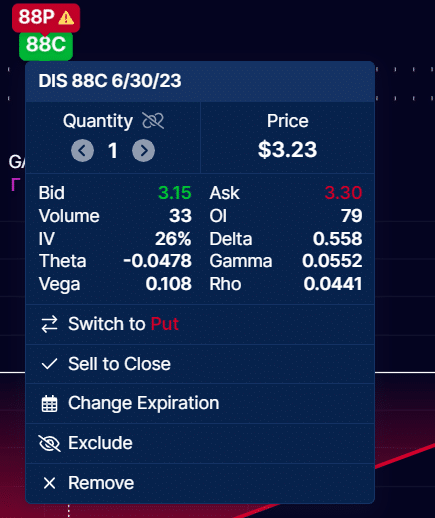
Source: optionstrat.com
And the Rho of the put option is -0.04 per share (recall that a long put has negative Rho).
For one contract (equivalent to 100 shares), we multiply the quoted Greeks by 100.
One call contract: 4.4 rho
One put contract: -4.0 rho
One lot straddle: 0.4 rho
The Rho of the put option and the call option almost canceled themselves out, giving the long straddle a negligible rho.
In other words, a change in interest rate will not affect the value of a long straddle.
The value of our example straddle is $576 because it costs $323 to buy the call option and $253 to buy one put contract.
If the interest rate increases by 1%, then the value of the straddle will increase to $576.40.
More realistically, say that the interest rate increased by 0.25%, then the value of the straddle would increase from $576 to $576.10 – assuming all other factors remain unchanged.
An $0.10 increase on a capital of $576 would amount to a 0.017% increase in the straddle value – quite negligible.
What is the effect of interest rates on calendar spreads?
Because the sensitivity to interest rates is different for the near-term option than the far-term option, there is an effect on the interest rate to the calendar spreads.
The far-term option will be more sensitive to interest rates than the near-term option.
A long call calendar will have positive Rho since the far-term call option has positive Rho. This is offset slightly by a negative rho from the short option – but not enough.
A call calendar will expand with a rise in the interest rate and narrow with a fall in interest rates.
It is the opposite of the long put calendar.
The far-term put option has negative Rho, which the positive Rho partially offsets from the short put.
However, the far-term Rho dominates since options with more time are more affected by interest rates.
Therefore a put calendar has negative Rho.
As interest rates rise, the put calendar decreases in value.
As interest rates decrease, the put calendar increases in value.
In terms of changes in interest rates, a put calendar behaves like a long put.
A call calendar behaves like a long call.
This makes sense because a put calendar is dominated by its long put option.
Similarly, the call calendar is dominated by its long call leg.
The greater the spread distance in time between the near-term and far-term expiration of the calendar, the greater the sensitivity to interest rates.
A narrow-spread calendar will be less sensitive to interest rates with smaller values of net Rho.
A call calendar and a put calendar of the same strikes and expiration will have similar values for all the Greeks, except for Rho (which will be opposite for each).
Conclusion
The risk-free interest rate is one of the five inputs into the Black-Scholes model.
Rho measures the effect of interest rate on an option’s value.
Think of Rho as an option’s sensitivity to changes in the interest rate.
However, as an option Greek, it is relatively unimportant, and most traders will be more concerned with the other Greeks, such as delta, vega, theta, and gamma.
One reason why Rho is not so important is that interest rates do not change that often.
Even if it does, it will not change a lot all at once.
We hope you enjoyed this article about how and why interest rates affect options.
If you have any questions, please send an email or leave a comment below.
Trade safe!
Disclaimer: The information above is for educational purposes only and should not be treated as investment advice. The strategy presented would not be suitable for investors who are not familiar with exchange traded options. Any readers interested in this strategy should do their own research and seek advice from a licensed financial adviser.










