

Just when you thought you had it figured out with the first-order greeks, you find out there are second order greeks as well.
The first order greeks are the sensitivities of different factors to the price of an option.
Yet that is not all.
The second-order greeks are sensitivities affecting the first-order greeks, therefore indirectly affecting the price of an option.
This article will explore all of the second-order greeks and talk about some of their sensitivities.
We will also discuss the importance of second-order greeks in options trading.
This article will be a basic overview.
If you are curious about going deeper into one of these greeks or reviewing the first order greeks feel free to explore the links in this article.
Contents
- Why Are Second Order Greeks Important in Options?
- Gamma
- Vanna
- Vomma
- Charm
- Veta & Vera
- What About the Third Order Greeks?
- Do I Need To Monitor These Second Order Greeks To Trade?
- Concluding Remarks
Why Are Second Order Greeks Important in Options?
Second-order greeks are a fundamental part of options themselves.
In fact, without second-order greeks, an option can simply not exist.
For example, without second order greeks, one could sell a delta 30 call, which would be equivalent to shorting 30 shares.
While these are somewhat similar on inception, the payoffs at expiration are very different, as shown below.
The black line shows our short call, and the yellow line shows the short shares.
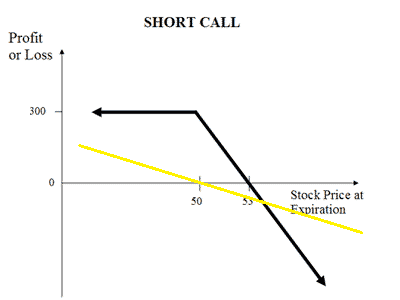
So underestimating the importance of second-order greeks is never a good idea.
Nevertheless, as they affect the first order greeks, their importance is naturally less than the first order greeks.
Some options gurus will attempt to sell services or just appear smart by rattling off the second-order greeks constantly, with almost no regard to the basic first-order greeks.
This is like buying all the best golf equipment without ever taking a golf lesson.
Sure, you may look good in the parking lot, but that doesn’t mean much.

Source: Golf.com
If you are reading this and are new to the first order greeks, here are some refreshers first.
Review of Delta
Review of Vega
and finally – Theta
Now, let us introduce our second-order Greeks!
Gamma
Gamma measures the rate of change of an options delta for a given change in an options price.
Remember our graph above of the short delta 30 call?
It looks so much different from the short shares because as the price of the underlying changes, the option’s delta changes as well.
This is gamma in effect.
If there is one-second order Greek to learn inside and out, it is gamma.
This is as it has very large effects on the moves in the price of an option.
So much so that many learn about it along with the first-level greeks.
Gamma also has a very strong relationship to theta.
As the buyer of an option, we are buying gamma and selling theta.
As an options seller, we are selling gamma and buying theta.
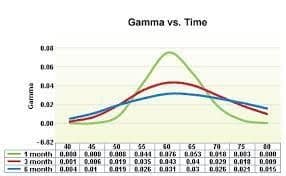
Source: Options Education Org
As we can see, at-the-money options with very little time to expiry have the most gamma.
These also have the most theta.
For all traders, especially those trading shorter-dated options, understanding gamma is a must.
Vanna
Vanna measures the change in delta for any given increase or decrease in the level of implied volatility.
The options that have the most Vanna are out-of-the-money options.
This is because a delta 50 option will not change if the level of implied volatility increases.
In contrast, a delta 10 option will gain a significant amount of delta if the level of implied volatility goes drastically higher.
We can see this Vanna exposure from the chart below.
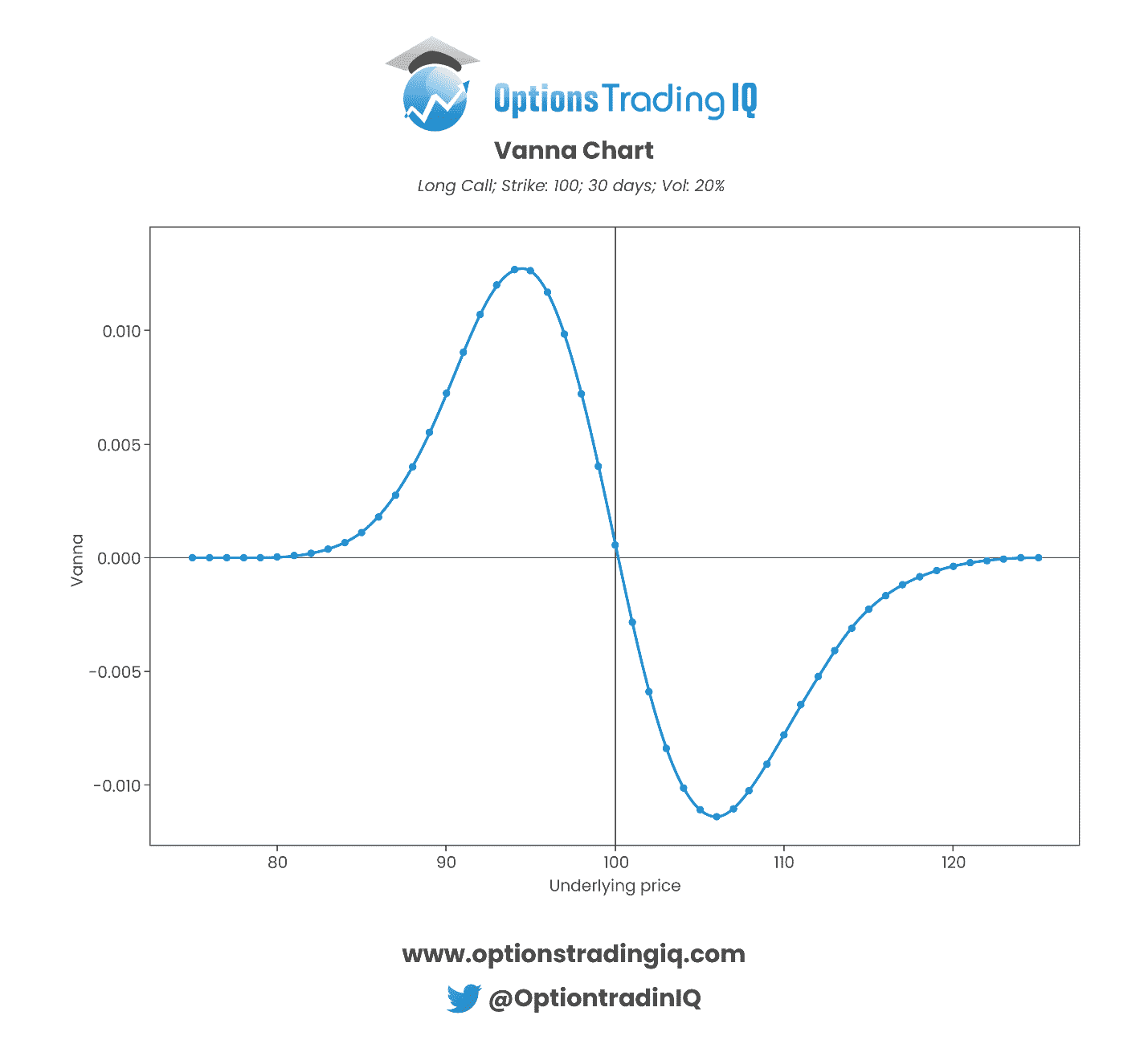
Therefore for at-the-money options and small positions, Vanna is not too important.
If you are trading naked out-of-the-money options, especially with large positions, make sure you know Vanna risk.
Vomma
Vomma measures the rate of change in an options vega for a change in implied volatility.
We can see from below the chart that Vega, Vomma is highest for out-of-the-money options.
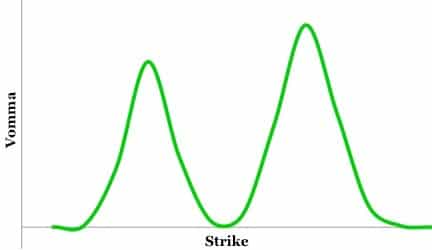
Source: My Options Course
Charm
Charm measures the rate of change in an options delta for a given passage of time or theta.
It is also commonly referred to as the delta decay of an option.
Charm is also very similar to Vomma and Vanna in that it affects out-of-the-money options the most.
It also affects shorter-dated options the most, as these decay the fastest.
Charm can be very important for delta hedgers or people who want to maintain constant exposure for out-of-the-money options.
Even if the price does not move, these options will lose their delta.
This can result in being over hedged if you are short or unable to take full advantage when a move comes if you are long.
Veta & Vera
Veta measures the change of vega with time (theta).
Vera measures the change in the rate of rho with respect to volatility.
Veta and Vera are two of the second-level greeks that are not commonly used.
Even the first order greek of Rho has been of little importance due to how low-interest rates are.
That being said, if interest rates were to move dramatically, longer-dated options would be affected.
What About the Third Order Greeks?
Just as there are second-order Greeks, there are also third-order greeks.
For the average retail trader, these will have little direct significance.
Focusing on these will most likely confuse someone further and distract them from the more important greeks.
Though for building models and higher-level finance, they are relevant.
Do I Need To Monitor These Second Order Greeks To Trade?
For most beginner traders, except for gamma, it is not necessarily to be too concerned with calculating your second-order greeks.
These second-order greeks can often have negligible effects for risk-defined positions such as iron condors and tight verticals.
Hence sometimes, a strong understanding, while helpful, may not be necessary.
Despite this, it is critical to understand at the least that the first-level greeks are not constant and will change over time.
This may result in some very different greek exposures as a trade progresses.
By monitoring your first-order greeks as a trade progresses, you can adjust for the effects of second-order greeks as the trade progresses.
This can help reduce variance and limit the risk on a position.
Concluding Remarks
The second-order greeks are a very important component of options themselves.
While they are naturally less important than the first-degree greeks they are derived from, they still explain why options exposures change over time.
Depending on the position’s structure, time to expiry, and delta, a position may have a minimal or relative significant exposure to these second-degree greeks.
Understanding a little about them and how they affect our main greeks can help us manage the hidden risks that a trade might have.
Trade safe!
Disclaimer: The information above is for educational purposes only and should not be treated as investment advice. The strategy presented would not be suitable for investors who are not familiar with exchange traded options. Any readers interested in this strategy should do their own research and seek advice from a licensed financial adviser.










