

When we first learned to adjust option strategies, we learned to move option legs around to decrease the position delta.
Making sure the delta is within an acceptable range is the most important step in managing the risk in an option trade.
The second priority is to manage the vega value.
There are multiple ways to reduce delta.
How do you pick between these different possible ways to adjust?
In this article, we will learn how to consider the implied volatility effects when making adjustments decisions.
Contents
Iron Condor Example
Suppose a trader has sold an iron condor on the RUT index on March 3, 2023.
Date: March 3, 2023
Price: RUT @ 1906
Buy one March 31 RUT 1760 put @ $8.70
Sell one March 31 RUT 1780 put @ $11.10
Sell one March 31 RUT 2020 call @ $7.45
Buy one March 31 RUT 2040 call @ $4.80
Credit: $505
The payoff graph and the Greeks are as follows:
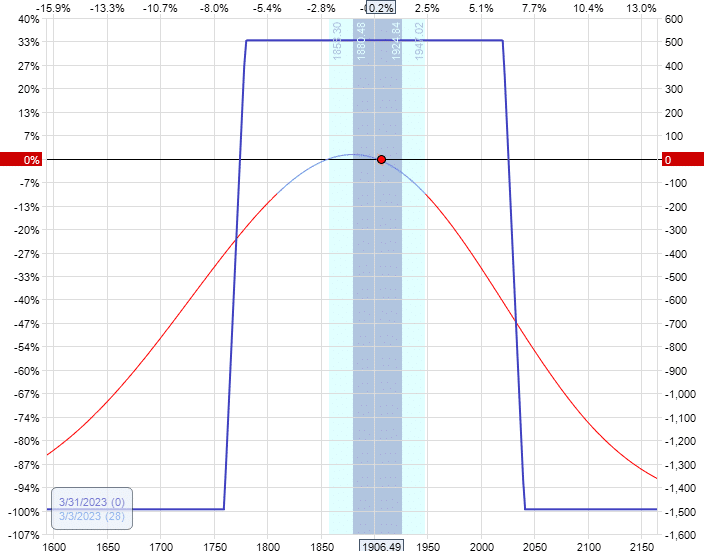
Delta: -1.97
Vega: -44.05
Theta: 16.68
An iron condor has negative vega, which means that it will benefit if the volatility of the underlying decreases (if all other factors remain the same).
By the same token, an increase in volatility would be a reduction in P&L.
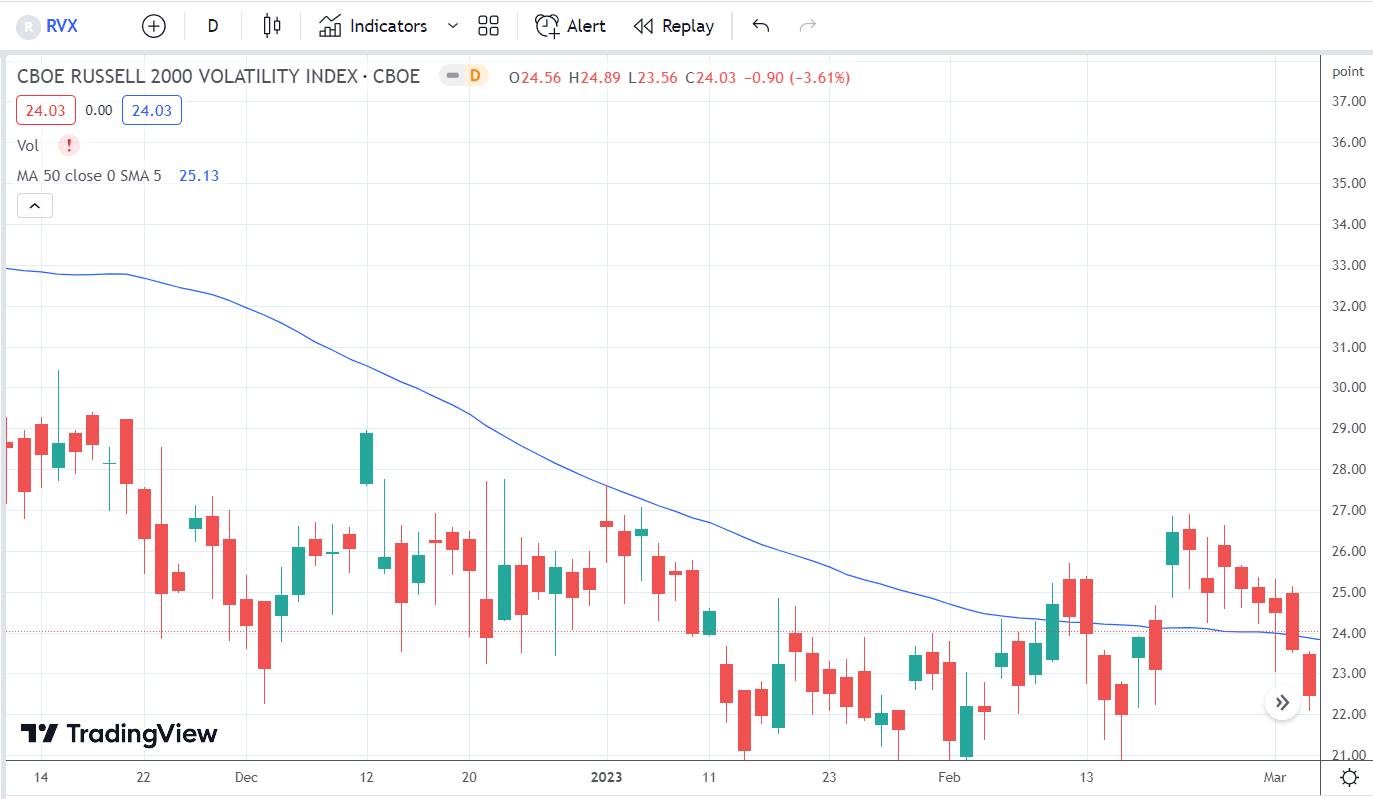
The volatility of the RUT index can be seen by watching the RVX, which is around 23 at the time.
A week later, on March 10, the put side was threatened because the price had moved down a lot:
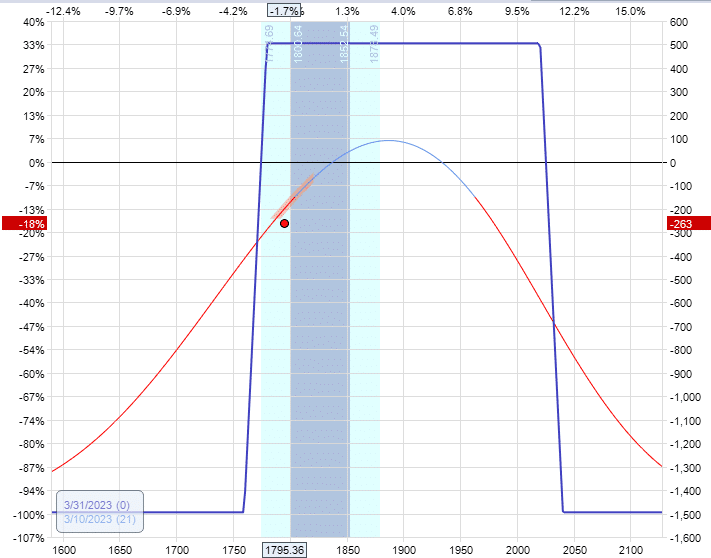
The Greeks of the position are:
Delta: 5.58
Vega: -12.34
Theta: 2.65
P&L: -$262.50
The standard adjustment would be to roll the put spread down to the 1690/1670 strikes for a net debit of -$410.
Buy to open March 31 RUT 1670 put @ $12.20
Sell to open March 31 RUT 1690 put @ $15.55
Sell to close March 31 RUT 1760 put @ $33.85
Buy to close March 31 RUT 1780 put @ $41.30
The resulting graph and Greeks would be as follows:
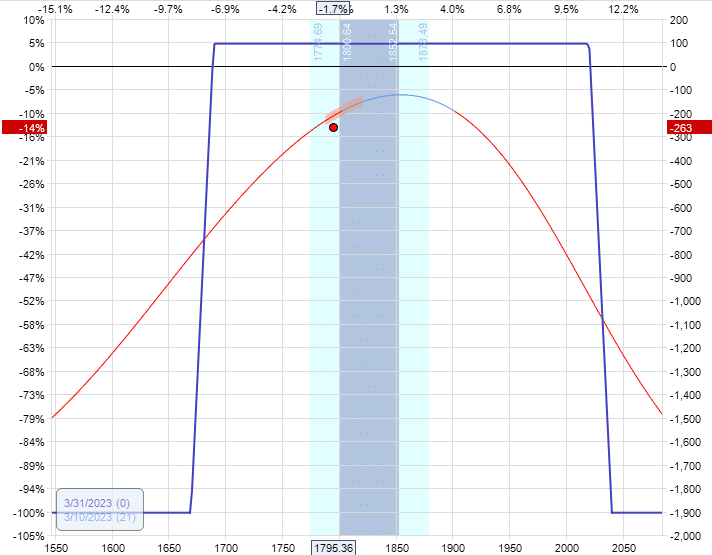
Delta: 2.83
Vega: -18.09
Theta: 9.32
It does have the desired effect of reducing the delta by about a half, from 5.58 to 2.83.
However, the vega increased in magnitude from -12.34 to -18.09.
This makes the resulting condor even more sensitive to volatility changes.
If the volatility of RUT continues to increase, it will not benefit the condor.
Alternate Adjustment
Another option is to purchase an at-the-money put debit spread that is further out in time.
For example, buying the 1800/1785 put debit spread with 42 days-to-expiration.
Sell April 21 RUT 1785 put @ $54.50
Buy April 21 RUT 1800 put @ $60.95
Debit: $645
The resulting graph and Greeks are:
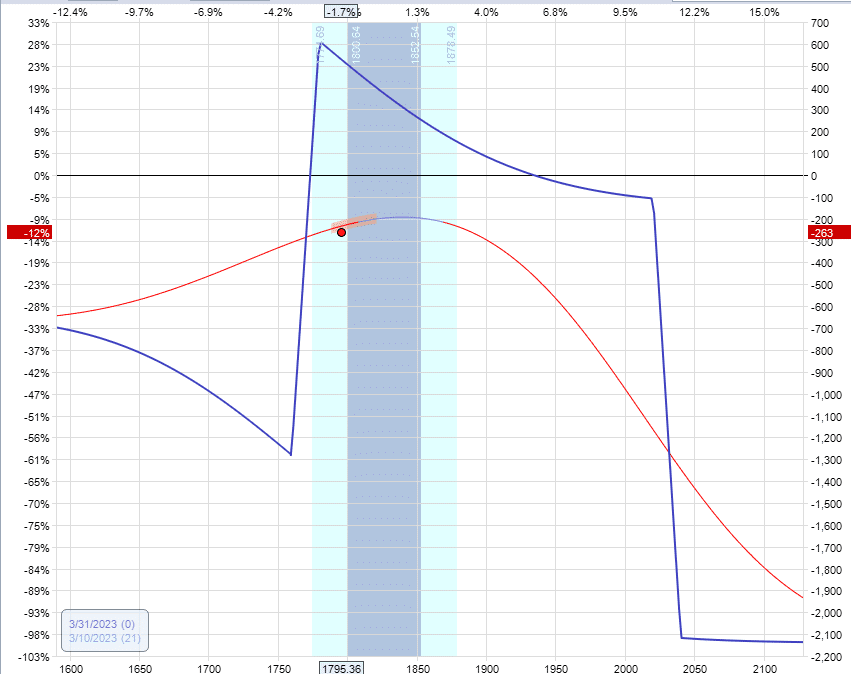
Delta: 1.70
Vega: -9.46
Theta: 4.10
It also has the desired effect of decreasing the delta value.
It increased theta, but not as much as rolling the put spread.
However, it decreased the vega to make the condor less sensitive to an increase in volatility.
Butterfly Example
Suppose we started with an at-the-money put broken-wing-butterfly on January 19, 2023, on the SPX.
Buy two February 24 SPX 3830 put @ $60.95
Sell four February 24 SPX 3900 put @ $85.60
Buy two February 24 SPX 3965 put @ $115.40
Net debit: $1030
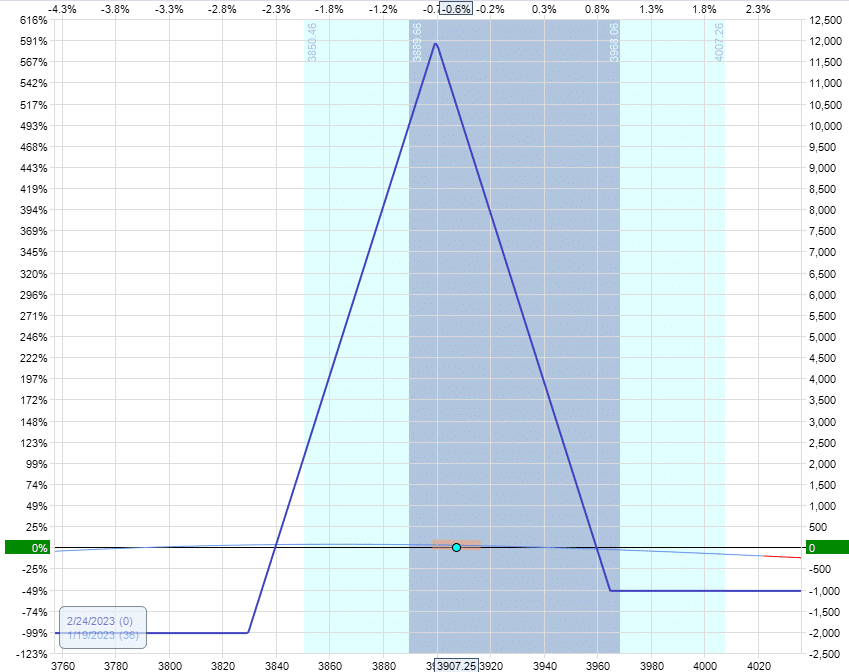
Delta: -0.99
Vega: -73.63
Theta: 19.77
Vega/Theta: 3.7
And the market goes up.
Near end-of-day on Friday, January 20, the trade requires an adjustment.
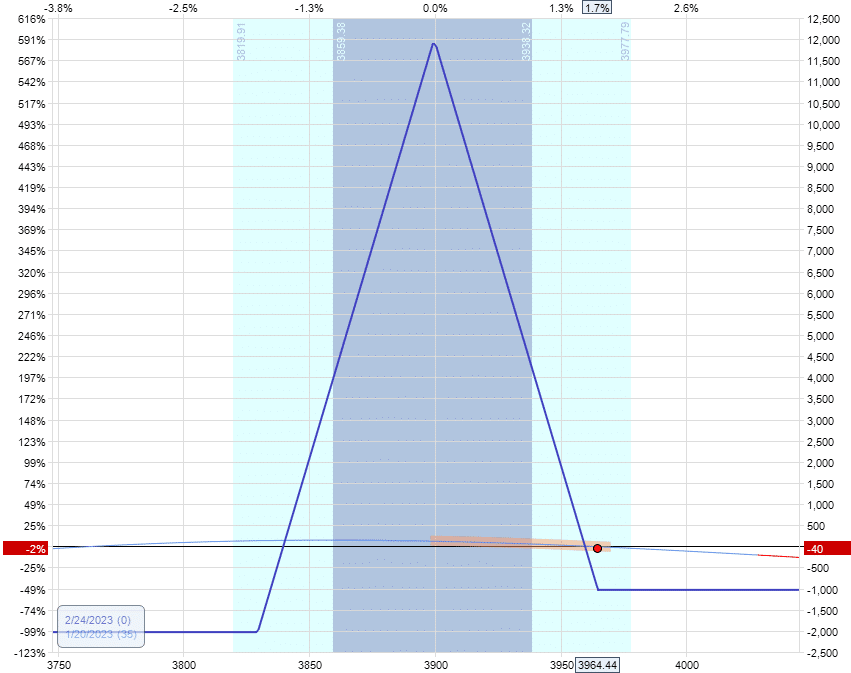
Delta: -2.76
Vega: -56.90
Theta: 17.88
Vega/Theta: 3.2
One can perform the Reverse Harvey adjustment.
Or, in this case, we opt to add a structure above the market. Do we add butterflies or calendars?
Let’s look at both choices.
Adding Butterflies
We add another butterfly for a debit of $2690 like this:
Buy two February 24 SPX 3930 calls @ $113.25
Sell four February 24 SPX 4000 calls @ $72.75
Buy two February 24 SPX 4060 calls @ $45.70
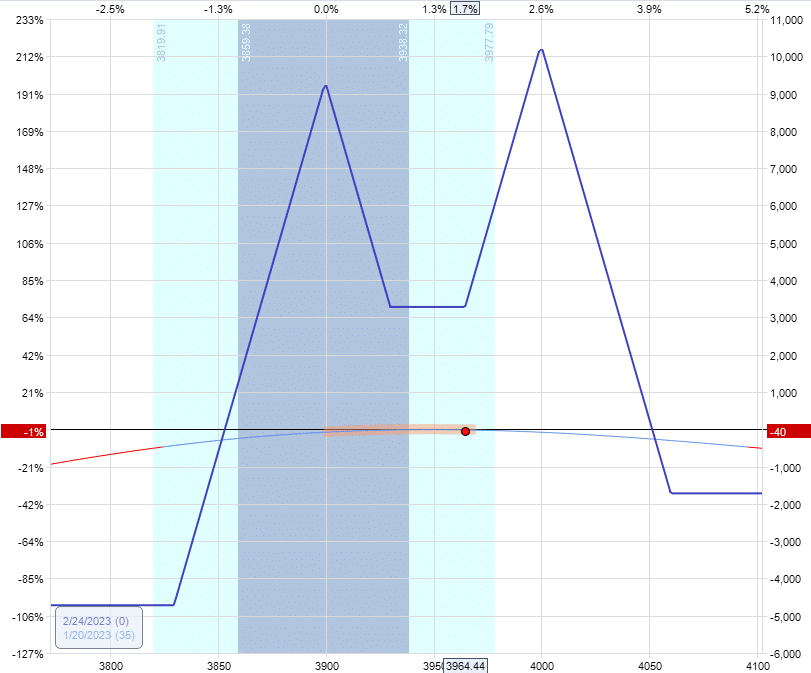
Delta: -0.85
Vega: -147.30
Theta: 36.50
Vega/Theta = 4
Adding Calendars
Or we can buy calendars for a debit of $1680 like this:
Sell two February 24 SPX 4000 calls @ $72.75
Buy two March 3rd SPX 4000 calls @ $81.15
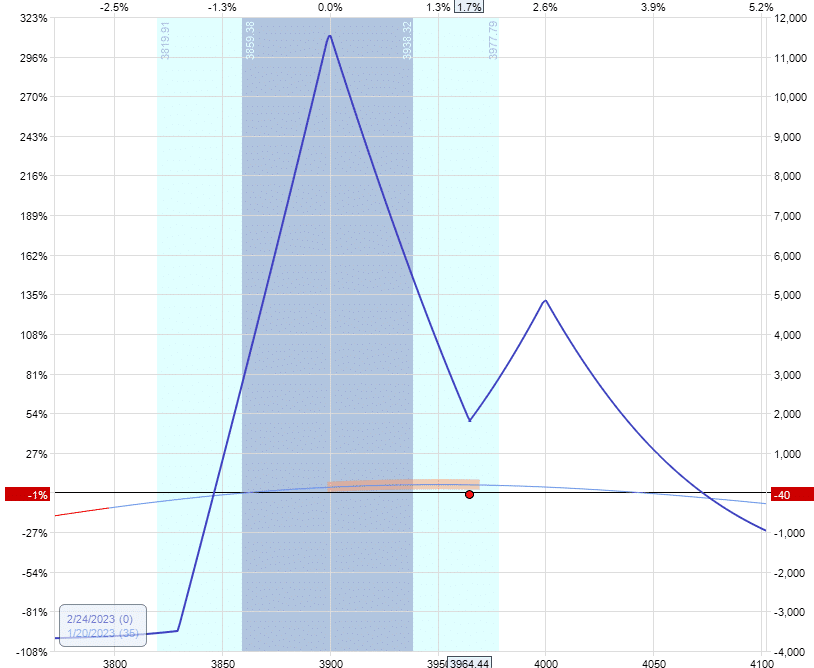
Delta: -0.81
Vega: 37.73
Theta: 38.10
Vega/Theta: 1
Comparison Analysis
Adding butterflies or calendars reduced the delta to the same degree.
The effects of theta and expansion of the profitable range are also about the same.
However, look at the resulting vega.
Adding calendars changed the sign of the vega.
Before adding the calendars or butterflies, the vega was -56.90.
After adding calendars, the vega turned +37.73.
After adding butterflies, the vega became more negative at -147.30.
Looking at the chart of VIX, it is at the low end of its range.
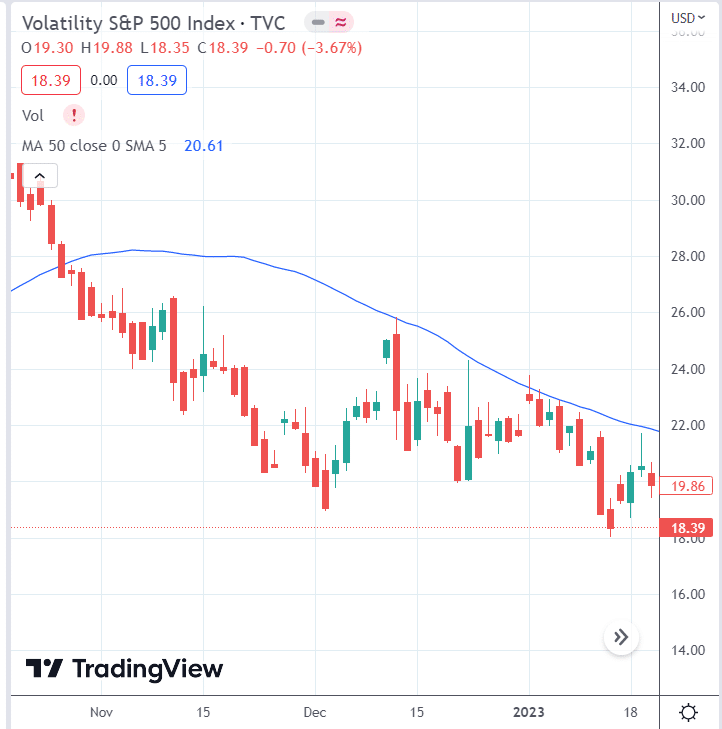
If VIX goes up or the market falls significantly, the volatility increase coupled with the large negative vega of -147 would harm the trade.
On the other hand, the trade would benefit from the positive 37.73 vega that the calendars give.
It depends of course on whether VIX goes up or down or what the market does, which no one knows.
Since we don’t know what volatility will do, we don’t want the trade to be too sensitive to volatility changes.
We want smaller numbers of vega (regardless of the sign).
The calendar reduces the magnitude of vega.
Adding butterflies increases the magnitude of vega.
You can see this in the vega/theta ratio. The resulting ratio is one after adding calendars.
The resulting ratio is four after adding butterflies.
Because butterflies are negative vega, calendars are positive vega.
The positive vega of the calendar hedges the negative vega of the original butterfly.
Frequently Asked Questions
Does the price of the calendar depend on volatility?
Yes, the price of the calendar is more when volatility is higher.
This is why the calendar likes it when volatility goes up; its value increases.
If we buy a calendar and its value increases due to an increase in volatility, we can sell it at a higher price for a profit.
Do butterflies cost more when volatility is high or low?
Butterflies cost more when volatility is low.
They cost less when volatility is high.
This is why many traders prefer to buy butterflies when VIX is high.
The butterflies are less expensive, and if volatility drops, the butterflies gain in value and can be sold for a profit.
Butterflies are negative vega. It likes it when volatility drops because that increases its price.
Under what conditions is it favorable to roll a calendar up in strikes?
If the price has gone up past the strikes of your calendar, consider rolling your calendar up as an adjustment. You can often get a credit for rolling the calendar.
When the underlying price increases, its volatility likely drops, meaning calendars become cheaper.
Selling your existing calendar and buying a cheaper one means you get a credit.
In the same line of reasoning, but in reverse, you can often roll a butterfly down for a credit.
When the price of the underlying goes down, the volatility increases, and the cost of butterflies decreases.
Selling the existing one and buying a less expensive one results in a credit.
Conclusion
When we make adjustments to range-bound strategies such as iron condors and non-directional butterflies, we use the adjustments to hedge delta and reduce price risk.
This is our primary concern.
Once this is achieved, our secondary concern is to hedge vega to reduce volatility risk.
In this article, we’ve seen considerations for doing this.
We hope you enjoyed this article about implied volatility for options adjustments
If you have any questions, please send an email or leave a comment below.
Trade safe!
Disclaimer: The information above is for educational purposes only and should not be treated as investment advice. The strategy presented would not be suitable for investors who are not familiar with exchange traded options. Any readers interested in this strategy should do their own research and seek advice from a licensed financial adviser.










