

Grab a cup of coffee and put on your thinking cap. Today we are going to do a deep dive into the world of synthetic stock strategies.
Contents
-
-
-
- Introduction to Synthetic Stock Strategies
- Synthetic Short Stock
- Synthetic Married Put
- Synthetic Covered Call
- Why Would Investors Sell In-The-Money Covered Calls?
- Wouldn’t the investor lose money if a stock is called away at a strike lower than the current stock price?
- How Can Investors Remember All These Equations?
- What Good Are All These Equations?
- Conclusion:
-
-
Introduction to Synthetic Stock Strategies
Let’s start with the following statement:
We can mimic the behavior of a long stock position by using options.
Why would we want to do this, you ask?
Because holding large shares of stock is capital intensive, some investors prefer to use the leverage of options.
Let’s mimic the behavior of stock in Tesla (TSLA) by buying a call and selling a put as in the following:
Date: May 26, 2023
Price: TSLA @ $193.17
Buy 1 June 30 TSLA $195 call @ $11.35
Sell 1 June 30 TSLA $195 put @ $12.18
Net Credit: $83
We actually get a net credit for initiating the trade, and the payoff graph looks as follows when inputted into OptionNet Explorer analytical software.
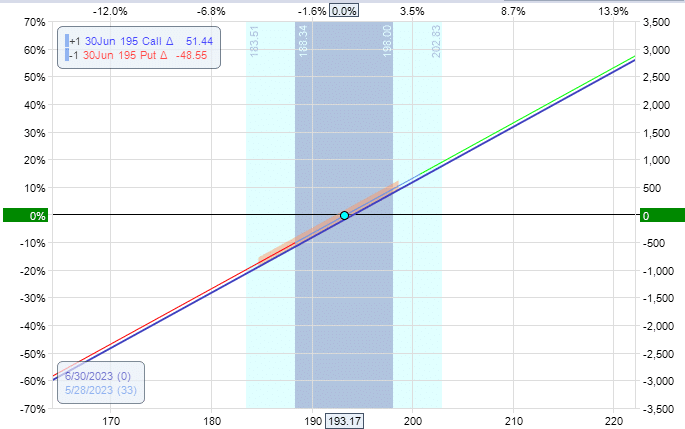
Just because we did not pay any money to enter the position does not mean we have no risk.
This is far from the truth.
Just like a stock position, this synthetic stock position has unlimited risk (up to the point when the TSLA price falls to zero).
And the reward is unlimited.
This position is called a “synthetic stock position” because it behaves very similarly (with minor differences) to having 100 shares of TSLA stock.
You can compare the payoff graph of 100 shares of TSLA stock below:
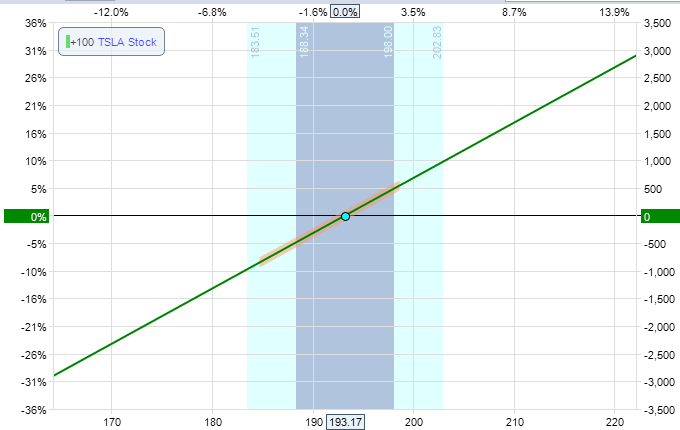
They look the same.
There is only a minor difference in the Greeks.
The delta for the stock position is always 100.
The stock position has gamma, theta, vega, and rho values of zero.
The stock’s delta is not affected by a change in the underlying price (as measured by gamma).
A stock does not lose value over time (as measured by theta).
And its stock price is not affected by its volatility (vega) or interest rate (rho).
The options position is affected by the Greeks.
Its Greeks, as reported by OptionNet Explorer, are:
Delta: 99.94
Theta: -2.53
Vega: 0.00
Gamma: 0.00
Vega and gamma are zero.
The vega of the long call option is 23.15.
The vega of a long put option of the same strike and expiration is the same value of 23.15.
But since we are selling the put option, we have -23.15 vega for our short put.
The net effect is a zero vega for the combined position.
The gamma of both the call option and the put option is 1.43.
But since we are buying the call and selling the put, both cancel each other out with a net gamma of zero.
Why, then, is theta not zero?
It is because we have a non-zero risk-free interest rate.
The option position has a positive rho value.
It benefits when the interest rate goes up.
The option position is more attractive than the stock position when the interest rate goes up because investors need to pay higher interest to raise capital to buy the stock.
The option position is less capital-intensive and becomes more attractive.
This also explains why the option position loses value with time (negative theta).
An investor choosing to invest in Telsa by buying the stock has to pay interest to raise capital.
Even if he has the money and does not need to borrow, he loses the opportunity to put that money in a risk-free interest-bearing vehicle.
In either case, he loses a bit of money due to interest.
Then why shouldn’t the option investor lose money?
The market is fair. It makes the option investor lose money via the negative theta.
What happens at expiration if the price goes up?
Suppose Tesla stock closed at $200 at expiration at the end of the day on June 30.
The stock position would have gained $683.
Because ($200.00 – $193.17) x 100 = $683.
Let’s see what would be the gain of the options investor.
The short put will expire worthless.
The call would be in-the-money, and the investor would exercise the call by buying 100 shares of Tesla at the strike price of $195 – paying $19,500 for 100 shares.
He paid only $19,417 because of the initial $83 credit he received at the start of the trade.
Since Tesla’s stock is now worth $20,000 at market value, he has a net gain of $583.
$20,000 – $19,417 = $583
The gain is $100 less than the stock investor’s, probably due to the slight negative theta.
However, on a $20,000 investment, there is a very slight difference between the stock and options positions.
What happens at expiration if the price goes down?
What happens if Tesla stock closes at $100 at expiration?
In that case, the stock investor would have lost $9,317.
($193.17 – $100) x 100 = $9,317
Let’s see how much the option investor would have lost.
The short put will be in the money.
This means that the investor will be assigned 100 shares of Tesla at $195 per share.
This is a debit of -$19500.
When offset by the $83 credit, the option investor paid $19417 for 100 shares of Tesla.
Since 100 shares of Tesla now have a market value of $10,000, that is a net loss of $9,417 for the investor.
Again, the options investor lost $100 more than the stock investor.
However, had we calculated the interest the stock investor would have paid to borrow the cash for the initial outlay of the investment, it probably would come close to the same.
The point is that the stock and option investors will have similar gains and losses because their two positions are synthetically equivalent.
Synthetic Short Stock
In the last example, we saw the case where an investor invests in a product that is expected to go up.
Suppose an investor wants to bet in the other direction and expects a stock to go down.
Instead of shorting the stock, the investor can use a synthetic option position to make the same bet.
This can be done by buying a put and selling a call:
Date: June 2, 2023
Price: ORCL @ $105.86
Sell 1 June 30 ORCL $106 call @ $3.55
Buy 1 June 30 ORCL $106 put @ $3.23
Net Credit: $32
We will put this option position on Oracle (ORCL) into OptionStrat for analysis:
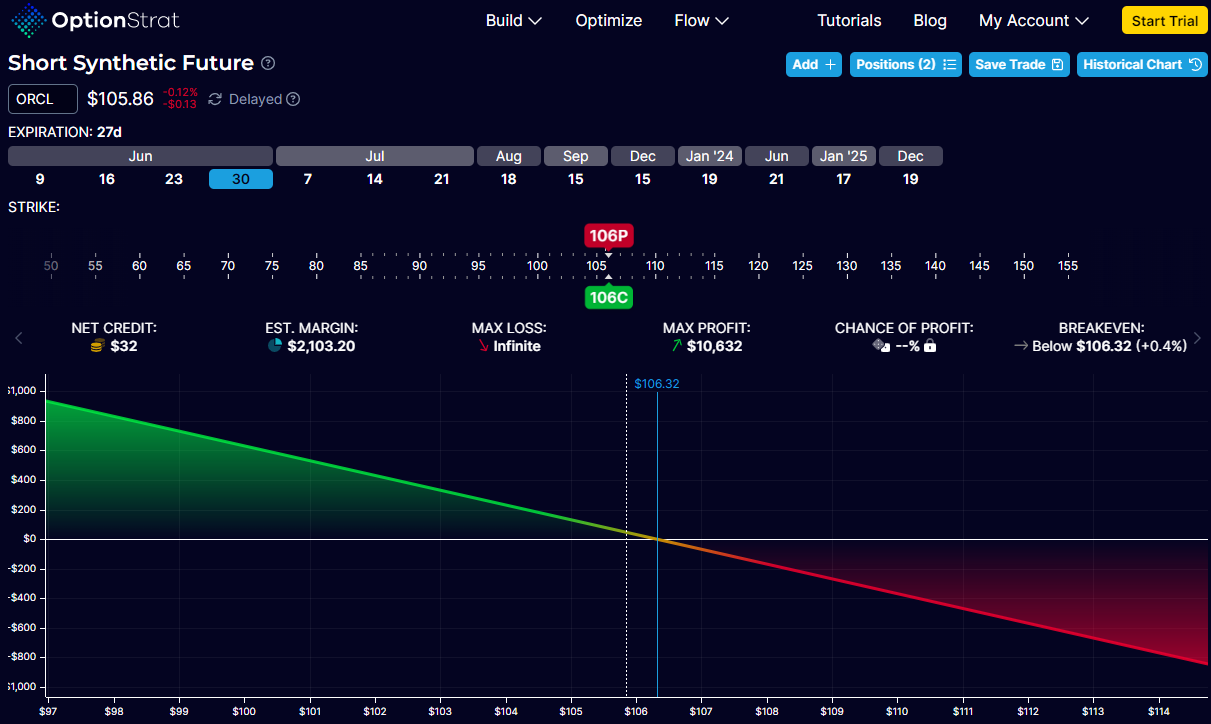
As you can see, the position benefits if the stock price goes down.
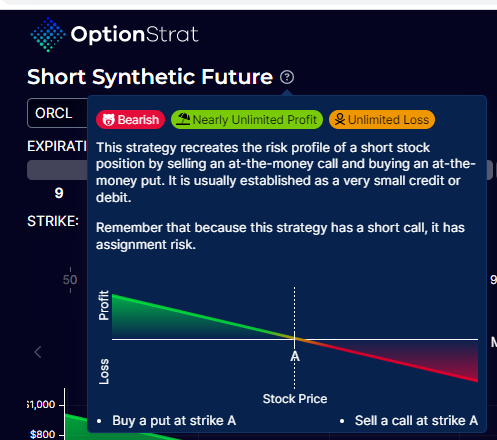
OptionStrat detected that this position is a “short synthetic” and provides an explanation…
Because we collected a small credit of $32 to initiate this options position, the stock can go up against us a little bit without losing money.
As calculated by OptionStrat, it shows that the stock price can go up to $106.32 before we start to lose money.
This is known as the break-even price.
The break-even price is denoted in blue, where the expiration graph crosses the zero profit horizontal.
To understand what that means.
Let’s imagine that the stock closed exactly at $106.32 at expiration.
In that case, the short call is in-the-money because its strike price of $106 is less than the current price.
The investor holding the short call must sell 100 shares at $106.
But the investor does not have 100 shares.
Therefore, he needs to buy them at the current market price of $106.32 and sell them at $106, losing about $0.32 per share.
For 100 shares, the investor had to give up $32 on the expiration day.
But recall that he had collected $32 at the start of the trade.
Therefore, he breaks even.
You can perform a similar thought experiment to see what happens if the stock price closes higher than $106.32 and what happens if it closes below $106.32.
Note that this option position consists of a naked short call, which can cause unlimited loss if the stock price goes up without end.
Because of the dangerous nature of such a position, it requires the highest level of options privilege in the account to place such an option position.
Synthetic Married Put
A married put is when a stock investor buys one hundred shares of a stock and protects it by buying one put option.
For example,
Date: June 2, 2023
Price: CRM @ $212.98
Buy 100 shares of CRM @ $212.98
Buy 1 June 30 CRM $210 put @ $4.95
Net Debit: $21,298 + $495 = $21,793
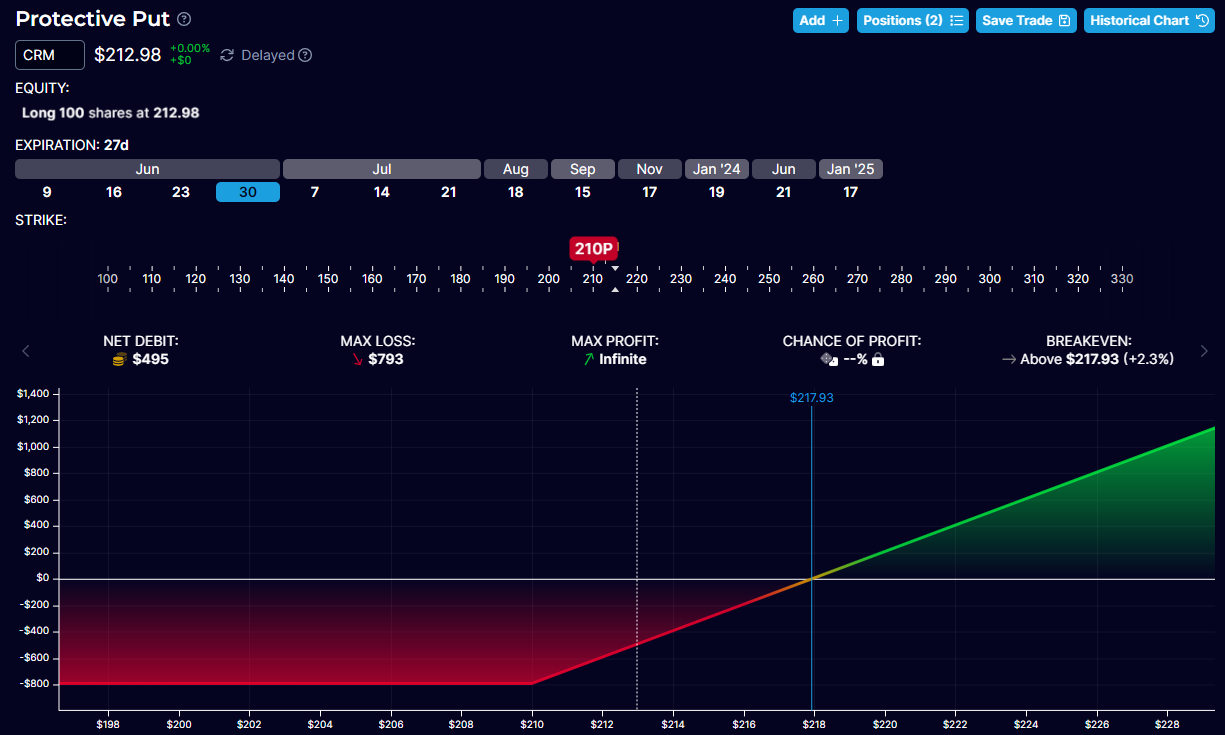
One can simulate this position by buying one June 30 CRM $210 call option at $8.88 or $888 for one contract.
If you compare the numbers on the two graphs, they are very similar:
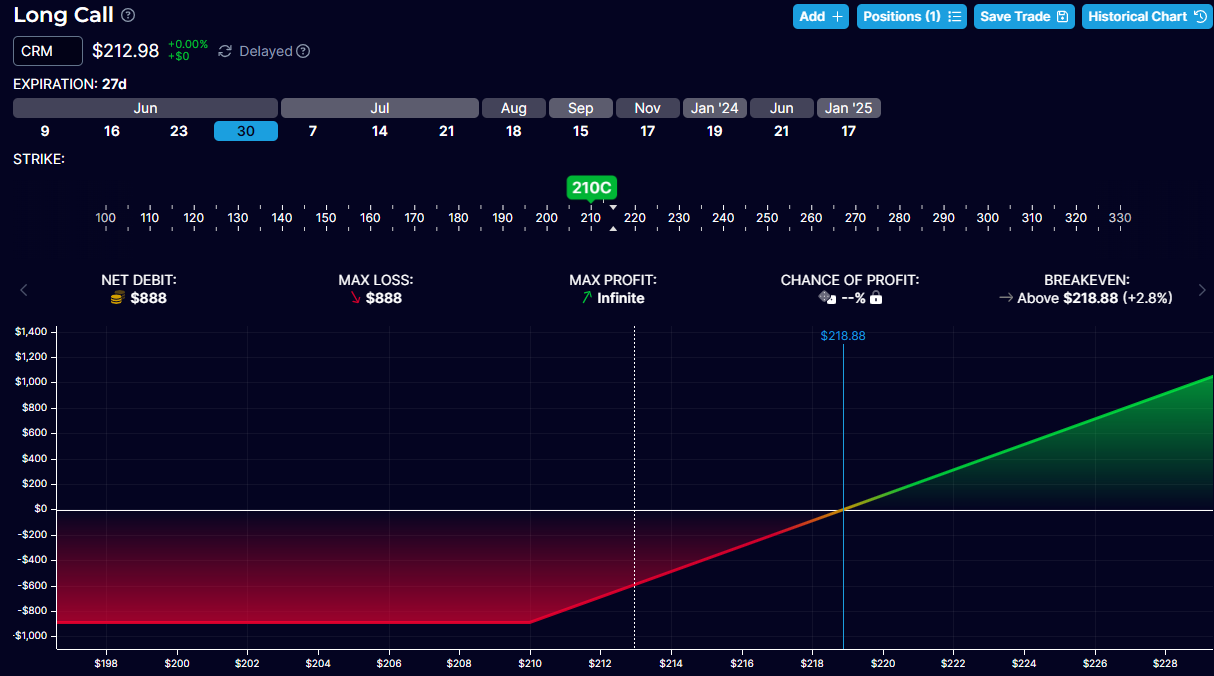
We say a long put plus long stock equals a long call of the same strike and expiration.
It is almost like an equation:
long put + long stock = long call
Synthetic Covered Call
A covered call is when a stock investor who owns one hundred shares of the stock sells a call option against it.
Here is the graph of 100 shares of Coca-cola (KO) plus a short call at $63, expiring in 27 days.
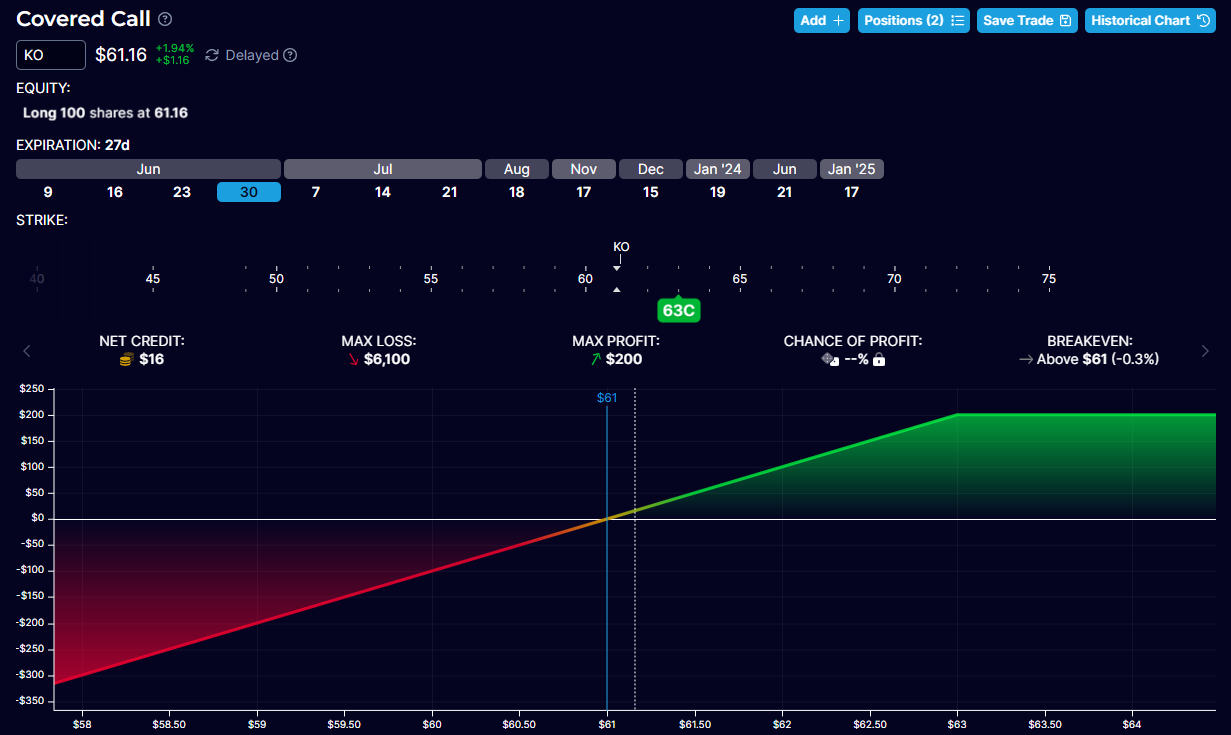
It is synthetically equivalent to a short put with the same strike and expiration:
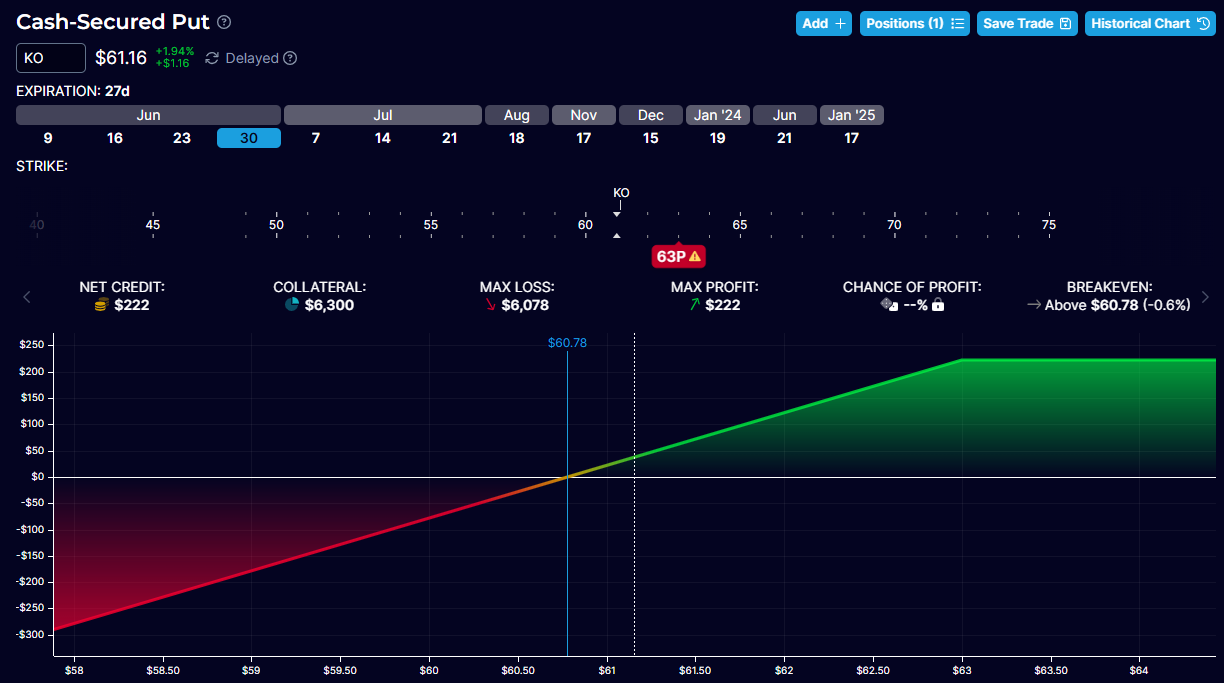
In the above, we see a short put with a $63 strike price when the current price of Cola-cola is $61.16.
This is an in-the-money short put, which investors do not typically do.
Many investors prefer selling short puts that are out-of-the-money such as the $59 strike put, to sell and collect a time premium on the option, as seen below.
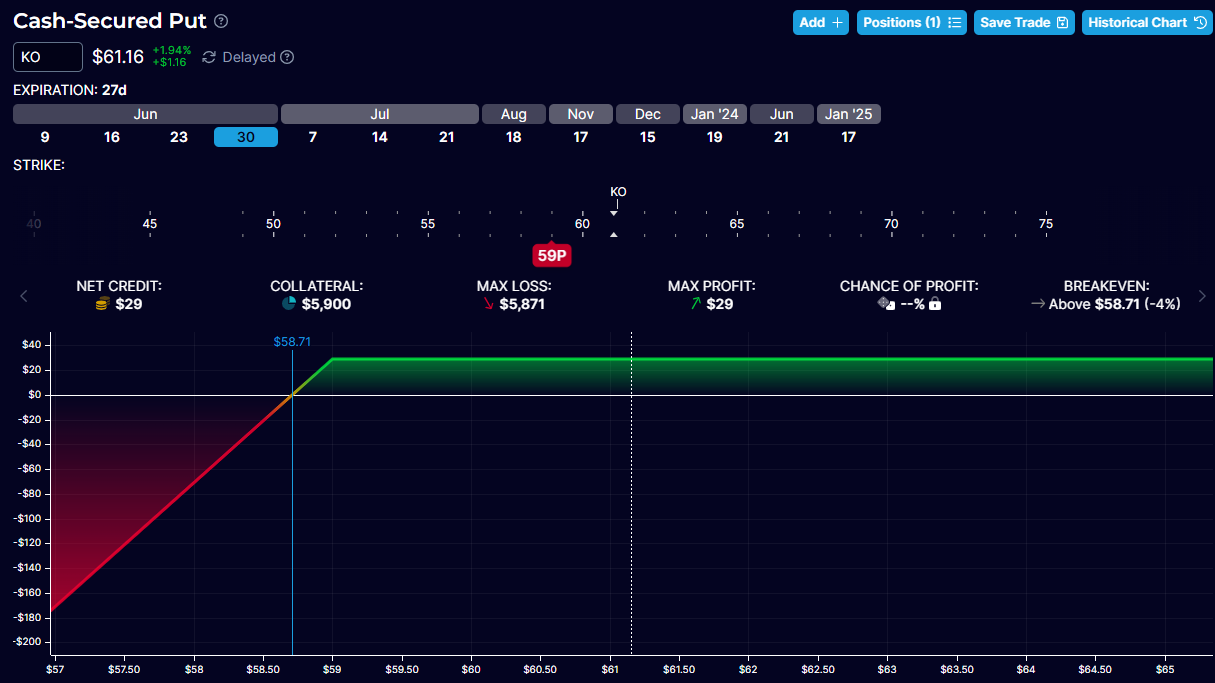
This is equivalent to an in-the-money-covered call.
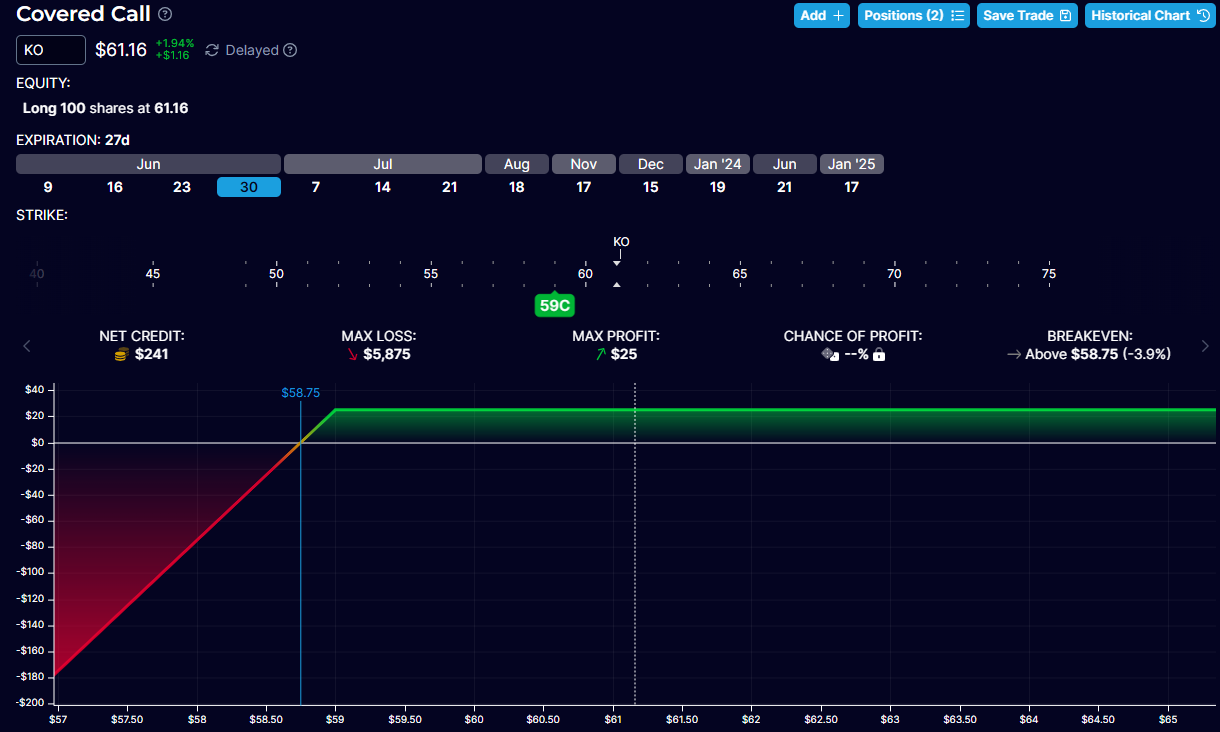
However, it is ironic that investors don’t like to sell in-the-money covered calls, which is equivalent to selling out-of-the-money cash-secured puts (which investors do like).
Why Would Investors Sell In-The-Money Covered Calls?
Investors like to sell out-of-the-money cash-secured puts for the same reason.
The two are synthetically equivalent.
They are selling to collect premiums.
In-the-money covered calls do have time premium in them (also known as extrinsic value).
When investors sell these options, and the option gets assigned, the investor gains the premium.
Selling in-the-money covered calls increases the chance that it gets assigned.
The investor may want to do this if they really want their stock to be called away.
Wouldn’t the investor lose money if a stock is called away at a strike lower than the current stock price?
No. Because the investor collected the credit by selling the covered call.
That difference from the strike price is baked into the credit of that call option.
Having stock called away at a strike price lower than the current price of the stock is just like having an out-of-the-money short put expire worthless.
In both cases, the investor gains the extrinsic value of the option.
On the contrary, the investor does not want the stock price to drop too far below the strike price of an in-the-money covered call.
If it is below the break-even point, this is when the investor loses money – the same as if a short put goes in the money.
To better understand, look at the break-even points of the graphs in the above Coca-Cola example.
How Can Investors Remember All These Equations?
Remember that if you have an option and hedge it with a stock, you get the accompaniment option.
For example, you have seen in the married put example that if you have a long put (which is bearish) and hedge it with long stock (which is bullish), you get the long call.
long put + long stock = long call
Now for the covered call example, we have:
long stock + short call = short put
If we add short stock to both sides of the equation:
long stock + short call + short stock = short put + short stock
The long and short stock cancels out, and you are left with,
short call = short put + short stock
This is saying that if you have a short put (which is bullish) and hedge it with short stock (bearish), then you get the short call (which is the companion option to the short put).
Short put + short stock = short call
In the very first example of synthetic long-stock, we had:
Long call + short put = long stock
If you mathematically manipulate it by adding a long put to both sides of the equation,
Long call + short put + long put = long stock + long put
The short put and long put cancel out, and you are left with the following:
Long call = long stock + long put
And add short stock to both sides of the equation,
Long call + short stock = long stock + long put + short stock
Which is the same as saying:
Long call + short stock = long put
In summary, long and short puts and calls can always be constructed using stock and its companion option:
Long put = long call + short stock
Short put = short call + long stock
Long call = long put + long stock
Short call = short put + short stock
What Good Are All These Equations?
Aside from academic curiosity, it is used to prove that an iron butterfly is synthetically equivalent to an all-put butterfly.
An iron butterfly is constructed with these options,
one long call
one short call
one short put
one long put
If we replace the long call with its stock equivalent:
one long put + long stock
one short call
one short put
one long put
And replace the short call with its stock equivalent:
one long put + long stock
one short put + short stock
one short put
one long put
The long stock and the short stock cancels, and we are left with an all-put butterfly,
one long put
two short puts
one long put
Which looks very similar to this:
Since an iron butterfly is just an iron condor with the short strikes placed together at the same strike, one can similarly prove that an iron condor is synthetically equivalent to an all-put condor, which is synthetically equivalent to an all-call condor.
Conclusion:
You didn’t know that you were going to do some algebra today, did you?
I told you we were going to do a deep dive into synthetics today.
We hope you enjoyed this article on synthetic stock strategies.
If you have any questions, please send an email or leave a comment below.
Trade safe!
Disclaimer: The information above is for educational purposes only and should not be treated as investment advice. The strategy presented would not be suitable for investors who are not familiar with exchange traded options. Any readers interested in this strategy should do their own research and seek advice from a licensed financial adviser.










