

When we first learned about options, we learned how the option’s value is dependent on the strike price in relation to the underlying price.
We also learned that as the price of the underlying asset changes, the value of our option also changes.
But other factors besides price movement can affect the price of the option.
Today, we will talk about the role of implied volatility and how it affects the option’s price.
Contents
Introduction
The implied volatility of an option represents the market’s expectation for the future volatility of the underlying asset.
This is the technical definition of implied volatility.
And I would admit, it is confusing when you first hear it.
What may be more useful is to think of implied volatility in a more intuitive sense.
Implied volatility is affected by the supply and demand of that option.
The higher demand tends to drive the implied volatility of that option higher.
In many software programs, implied volatility is denoted as “IV” for short.
To better understand IV, let’s look at the values given by ThinkOrSwim for Google’s underlying assets (GOOGL).
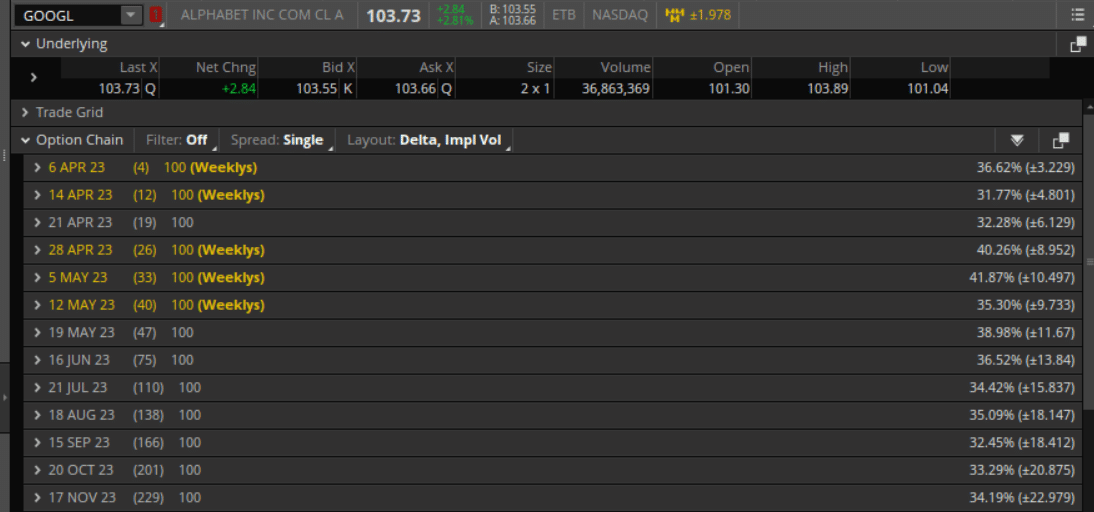
Source: ThinkOrSwim
The implied volatility for the various expiration cycles is shown as percentages in the right column.
For the April 14, 2023 expiration cycle (which is 12 days from now), the IV is 31.77%, which implies that Google can move plus or minus 4.8 points from now till April 14.
For the April 21 expiration cycle, the IV is higher at 32.28%, which implies that Google can move more from now to expiration.
Volatility Term Structure
It makes sense and is normal for later expirations to have higher IV since there is more time for the stock to move and more possibility for events to drive a larger price move.
There are sometimes event risks that can drive a particular expiration to have a higher implied volatility value.
For example, the May 5 expiration has a higher IV than the expiration before and after it.
It has an IV of 41.87%, whereas the expiration before has 40.26%, and the expiration after has 35.30%.
Why?
That is because Google announces earnings on May 4, and options expiring on May 5 are the options most affected by a large potential price move.
This results in those options having high implied volatility.
The high IV can be viewed in two ways.
And both ways are correct.
The high IV means there is greater demand for those options.
People are buying the May 5 put options to protect their Google shares of stock – just in case the price falls after the announcement.
Speculators are buying call options to potentially capitalize on a large upward move in price due to favorable earnings.
Second, the high IV is a gauge of how much the underlying price can potentially move. Google can potentially move a lot after the earnings report.
Hence the high IV.
Higher implied volatility reflects market expectations for greater potential price fluctuations in the underlying asset.
Implied volatility can also be used as a tool to gauge market sentiment.
If implied volatility is high, it suggests that traders are anticipating significant price movements in the underlying asset.
Conversely, low implied volatility suggests traders expect the underlying asset’s price to remain stable.
Individual option IV
Now let’s drill down into the individual options within the option chain for the April 21 expiration.
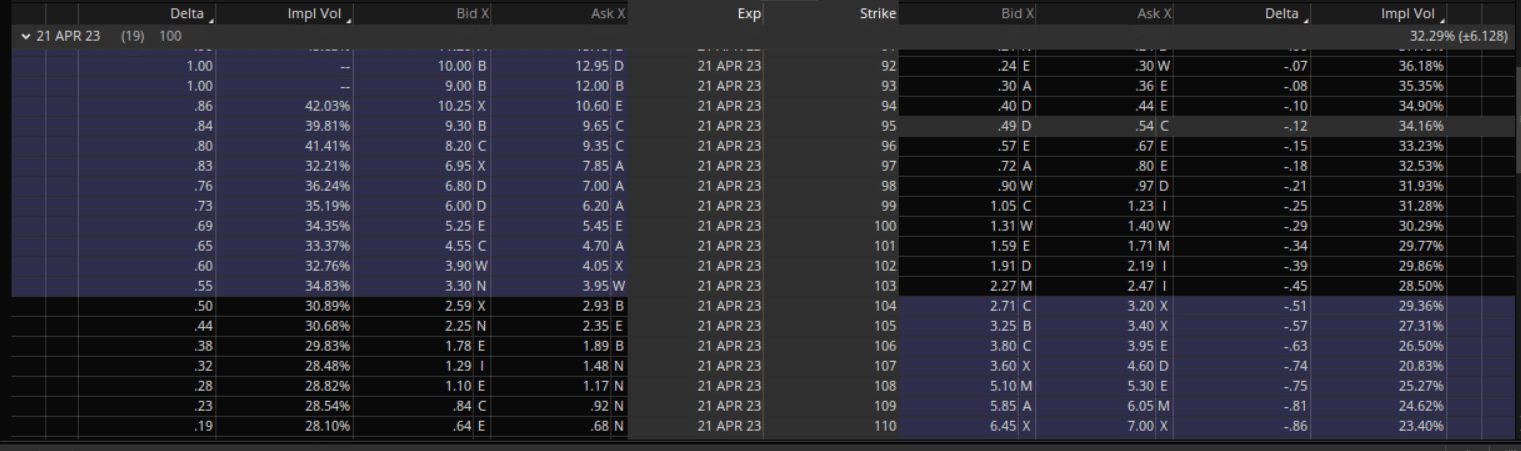
Source: ThinkOrSwim
Take a look at the highlighted $95 put option.
This out-of-the-money (OTM) put option has an implied volatility of 34.16%.
In contrast, the at-the-money put option for $103 has an implied volatility of 28.5%.
The IV goes up when we look at put options with strikes that are further away from the money.
This is typical.
Why?
The supply and demand dynamics of the options market impact implied volatility.
OTM put options may have higher implied volatility because they are often used as a form of insurance or protection against a potential downturn in the underlying asset.
As such, investors are typically more willing to pay a higher price for these options as they provide downside protection.
If IV is higher, then why is the $95 put option not more expensive than the at-the-money $103 put option?
Higher demand for items drives up the price, which makes them more “expensive.”
However, this “expensiveness” is not reflected directly in the actual price of the option, as seen in the bid/ask prices.
Because the bid/ask price of the option is largely driven by the underlying asset’s price in relation to the strike price.
The $103 put option is priced higher simply because $103 is closer to the current spot price of the GOOGL underlying stock, which is trading at $103.73.
The implied volatility is only a secondary effect on the option’s price.
The price of the underlying governs the main effect of an option price.
The Greeks
Delta is the most important Greek in determining an option’s value.
The Greek delta measures an option’s sensitivity to changes in the underlying asset’s price. Delta represents price risk.
The second most important Greek is vega.
Vega represents volatility risk.
The Greek vega measures the amount an option’s price is expected to change for every 1% change in implied volatility.
Vega represents an option’s price sensitivity to changes in implied volatility.
A large vega number means that the option price will change a lot as the implied volatility changes.
A long call option has positive vega. A long put option also has positive vega.
But you have a negative vega position if you sell a call option (we say you are short a call).
A short put option also has negative vega.
Option Structures and Implied Volatility
Option structures consisting of multiple options can result in either positive or negative vega as calculated by summing the vegas of their individual option legs.
The calendar option strategy has positive vega.
Its longer-dated option is being bought and has positive vega.
This positive vega is larger than the negative vega of the shorter-dated option that is being sold.
The iron condor is a negative vega strategy.
If an option position has positive vega, it will benefit if implied volatility increases (assuming that the other factors affecting price remain the same).
The calendar price will increase as implied volatility increases.
If implied volatility rises, a trader who bought a calendar for a $0.32 debit will benefit because the price has risen to $0.50.
An iron condor has negative vega and will benefit when implied volatility goes down.
Its P&L (profit and loss) increases as implied volatility goes down.
If a trader sells an iron condor for $1.00 credit and the value of that condor decreases to $0.50 due to a drop in implied volatility, that benefits the iron condor trader since they can buy back the condor at a lower price than what they sold it for.
Now you see how options traders use implied volatility to develop trading strategies.
They buy options when implied volatility is low and sell when it is high.
They sell options when implied volatility is high and buy them back when implied volatility drops.
FAQs
Why do out-of-the-money (OTM) call options tend to have lower implied volatility?
You can see this example in the above screenshot of the Google option chain.
OTM call options may have lower implied volatility because they are less in demand compared to at-the-money or in-the-money call options.
OTM call options are considered riskier, as the underlying asset must increase significantly in value for the option to have any value at expiration.
As such, investors may be less willing to pay a higher price for these options, resulting in lower implied volatility.
OTM call options are typically used for speculative purposes instead of hedging or risk management.
OTM call options are often sold by covered call writers.
The combination of these two dynamics results in less demand for OTM options in relation to supply.
What is the difference between implied volatility and historical volatility?
Implied volatility is not the same as historical volatility.
Historical volatility, also known as realized volatility or statistical volatility, is calculated using the actual price movements of the underlying asset over a certain period in the past.
Historical volatility provides information about how much the underlying asset has moved in the past.
Implied volatility provides information about the expected level of future price movements.
Implied volatility is calculated by inputting option pricing information into the Black-Scholes model.
You can say that it is the volatility implied by the Black-Scholes formula based on option prices.
Hence the term “implied volatility.”
Another way to look at it is that historical volatility is backward-looking and implied volatility is forward-looking.
What are the other factors affecting the price of an option besides implied volatility?
Besides implied volatility, the value of an option is affected by the underlying price in relation to the option’s strike price.
Options price is also affected by the option’s time to expiration and, to a lesser extent, by the risk-free interest rate.
Conclusion
Implied volatility can be a complicated topic, with many factors affecting the value of IV.
The concrete example of looking at the options chain’s various values may help consolidate the understanding.
Nevertheless, you may need to read this article multiple times to pick up all the nuanced implications of implied volatility.
We hope you enjoyed this article about implied volatility in options trading.
If you have any questions, please send an email or leave a comment below.
Trade safe!
Disclaimer: The information above is for educational purposes only and should not be treated as investment advice. The strategy presented would not be suitable for investors who are not familiar with exchange traded options. Any readers interested in this strategy should do their own research and seek advice from a licensed financial adviser.











Thank you Gavin all the way in Australia, I live in Canada and your blog articles are proving to be very valuable in my journey of learning options.
Thank you for that sir, I really appreciate it , keep up the good job!
Thanks for the explanation.Do you offer any
paid subscription services using High IV options for collecting Premium.Thanks
Not at this time, sorry. I’ll be running a course next month on option selling strategies, so keep an eye out for that if you’re interested.
Hello Gavin
Many thanks once again for your excellent series on Option trading.
Lots of best wishes