

Contents
- Introduction
- Maximum Loss
- Maximum Gain
- Breakeven Price
- Payoff Diagram
- The Greeks
- How Volatility Impacts the Trade
- How Theta Impacts the Trade
- Risks
- Summary
Introduction
When an investor is long a call, he expects the stock price to rise above the strike price before expiration.
A call gives him a maximum gain of infinity; however, any experienced investor realizes that there is no value to holding infinity.
Therefore, he enters a call spread by selling another call at a higher strike price to recoup some of the premium paid for the initial call.
There are two drawbacks to consider while using a call spread:
- Selling a call at a higher strike price will not generate enough premium to offset the initial long call so the investor still ends up with a large net debit position.
- By selling a call, the investor is selling infinity to someone else. What if the stock breaks all resistance and rallies above the strike of the sold call?
A Christmas tree with calls partially alleviates some of these drawbacks.
A Christmas tree with calls is a three-legged strategy involving six calls. The investor starts with a long call at strike A, skips strike B, sells 3 calls at strike C, and buys 2 calls at strike D.
Note, only the strikes differ. All options share the same underlying and same expiration.
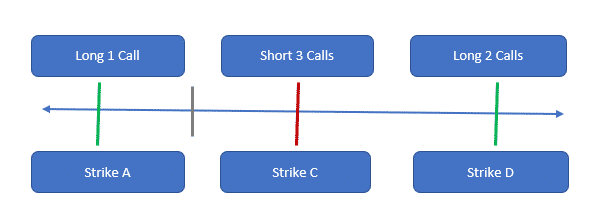
Let’s look at an example of Uber. The investor is long a call with strike of $37.5, sells 3 calls at strike of $38.5, and buys 2 calls at strike of $39.
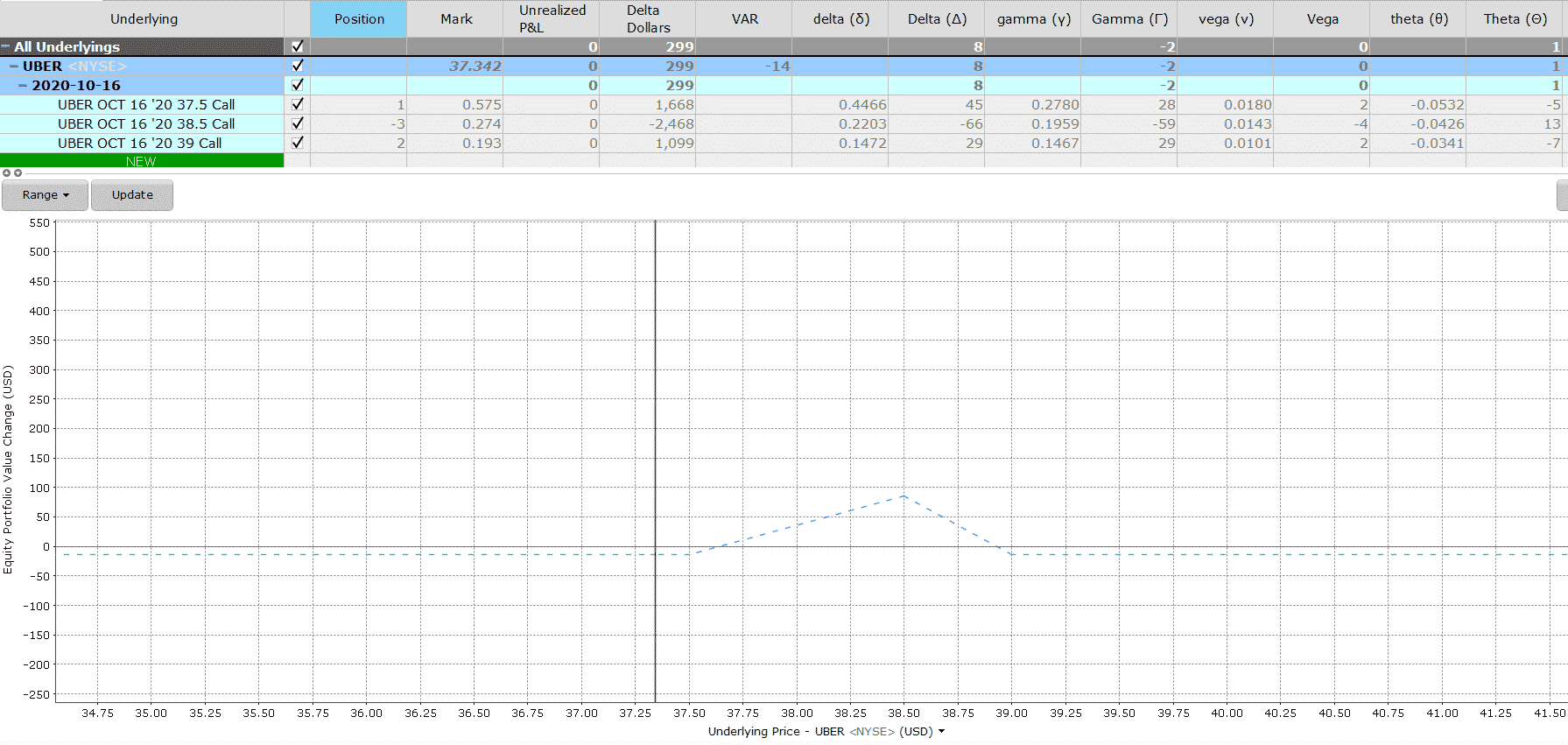
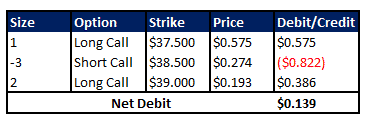
Before we look at the payoff of a Christmas tree with calls, let’s understand that this strategy will usually result in a small net debit i.e. the investor has to pay to enter the strategy.
In the uber example, the net debit is calculated as follows:
Compare this with the net debit of a regular call spread:
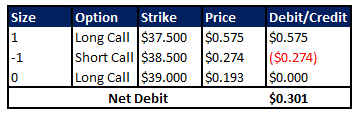
By selling additional calls, the investor recoups more premium to offset the cost of the initial call.
And by buying additional calls, the investor flatlines the payoff diagram so he is not exposed to further downside.
Maximum Loss
The investor is long 3 calls and short 3 calls. The most he can lose is the net debit paid.
In the example above, the maximum loss $0.139 per share.
Maximum Gain
The initial long call at the lowest strike price of $37.50 gives the investor unlimited gain potential if the stock rises above the strike.
However, the investor sold calls at $38.50 and reduces some profit potential above $38.50.
Therefore, the most he can make is the difference between the lowest strike price ($37.50) and the strike price of short calls ($38.50) minus the net debit to enter the strategy ($0.139).
The maximum gain is $0.861 per share in this example.
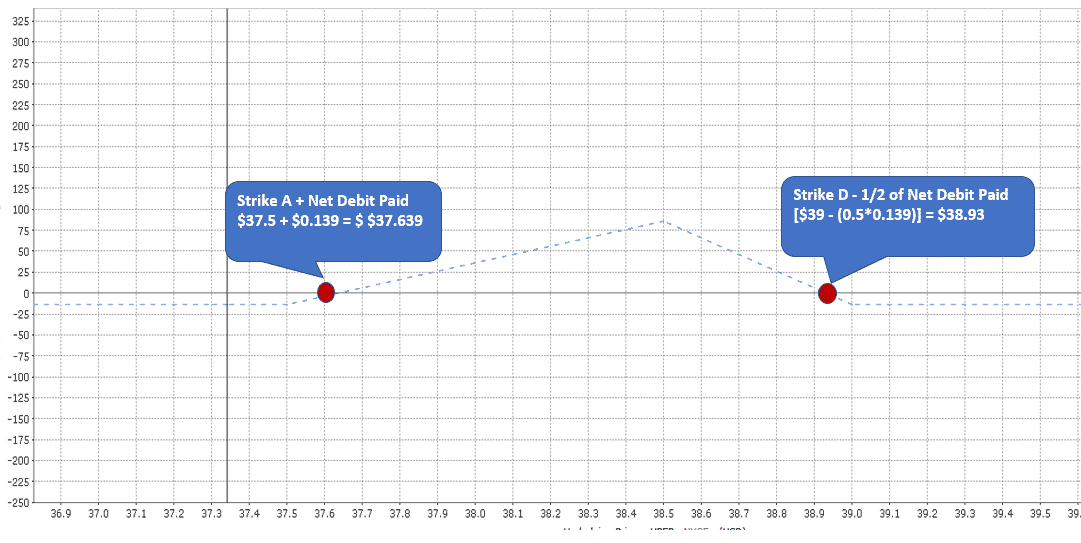
Breakeven Price
This strategy has two breakeven points.
- Lowest strike + net debit paid
- Highest strike – ½* net debit paid
Let’s look at the two breakeven prices:
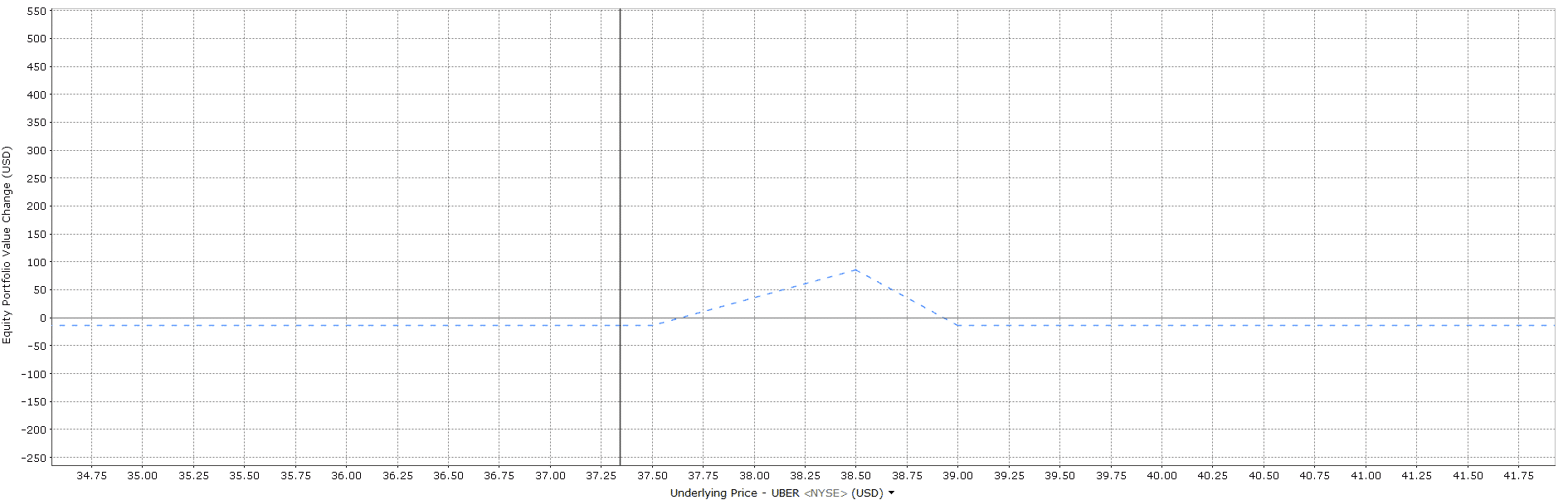
Payoff Diagram
Let’s look at the payoff diagram closely. We have 3 legs and 6 calls.
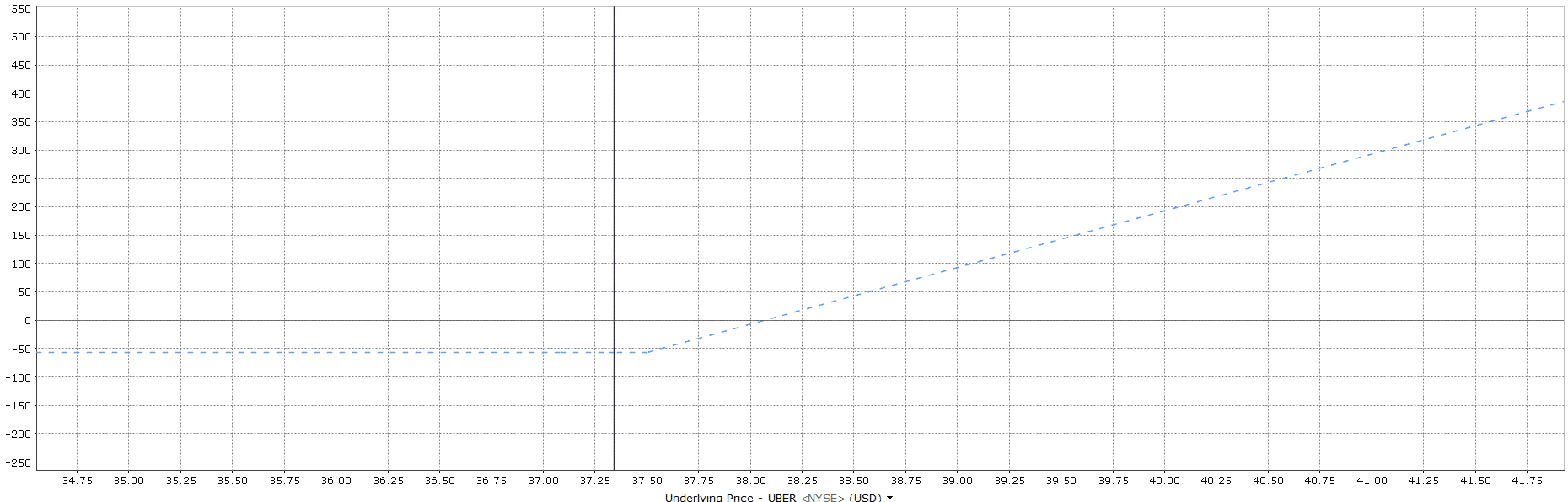
Leg 1: Long call at strike of $37.5 will have unlimited upside:
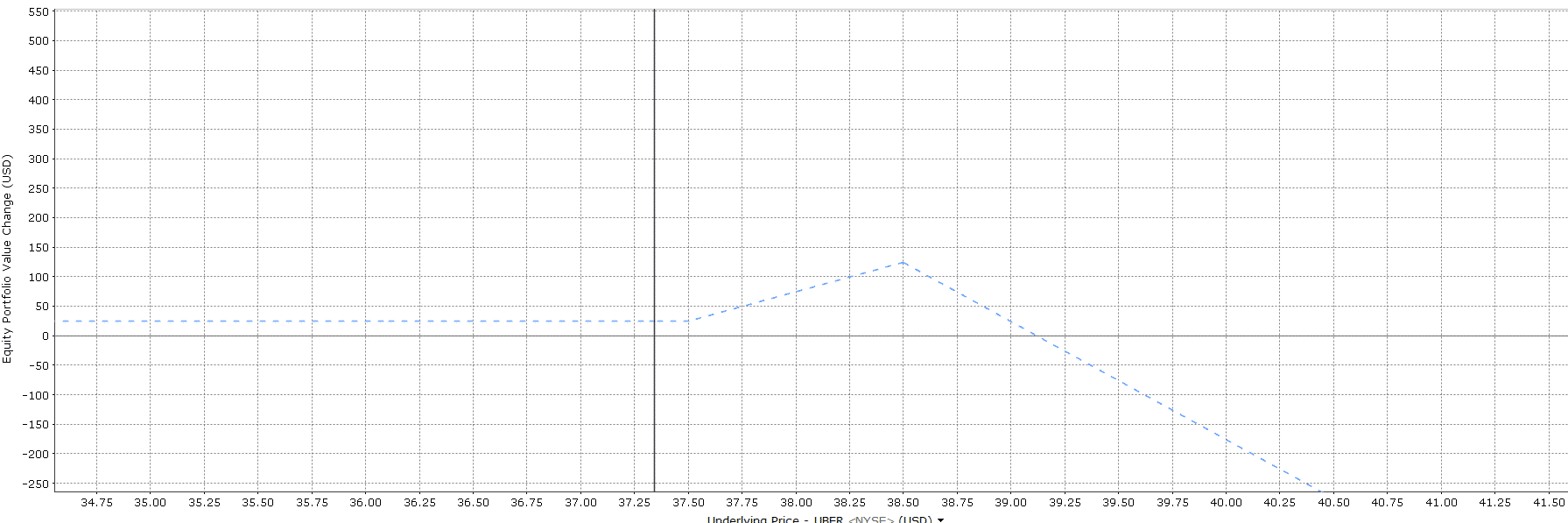
Leg 2: If the investor sells 3 calls at strike of $38.5, the payoff will change to:
Leg 3: And if the investor buys another 2 calls at strike of $39, the payoff will change to:
The Greeks
Delta
We know that delta measures the change in option price for a $1 change in the underlying stock.
It is directly proportional to moneyness and the more in the money the call is the more it behaves like a stock.
Long calls have delta between 0 and 1.
Short calls have delta between -1 and 0.
Delta of at the money calls is 0.5 for long calls and -0.5 for short calls.
The further in the money the call is set, the closer delta is to +1 for long calls and -1 for short calls.
And the further out of the money the call is set, the closer the delta is to 0.
In the example above, the investor has 3 long calls and 3 short calls with different strikes.
The initial long call has a delta of 44.65 per call.
The 3 short calls have a delta of -66.06.
And the 2 long calls have a delta of 29.40.
The overall position delta is 7.99.
The options behave like a long stock between the lowest call strike and the short call strike.
And the options behave like a short stock between the short call strike and the highest long call strike.
Gamma
Gamma is always positive for long options and negative for short options. It measures the rate of change in delta with respect to the change in stock price.
Gamma is the second derivative of the value function with respect to the stock price – Delta being the first derivative.
It is highest for at the money options because that is the point where delta changes fastest with changes in the stock price.
Therefore, the gamma of the initial long call with strike of $37.5 is the highest at 0.2782.
As the stock price moves away from the strike price (in either direction), gamma approaches zero and delta becomes less sensitive to changes in the stock price.
The investor is long 3 calls. One call being at the money (gamma of 0.2782) and two calls being out of the money (gamma of 2 * 0.1467 i.e. 0.2934). Total long call gamma of 0.5716
The investor is also short 3 calls with gamma of 3 * -.1960 i.e. -0.588.
The overall position gamma is -0.0164.
How Volatility Impacts the Trade
Long call options are long vega trades. They will benefit if volatility rises after the trade has been placed.
The initial long call with strike price of $37.50 has a vega of 0.018.
In other words, the value of the long call will increase by $1.8 if implied volatility increases by one point.
The three short calls with strike price of $38.50 have a vega of -0.0143.
In other words, the value of the 3 short calls will decrease by 3 times $1.43 i.e. $4.29 if implied volatility increases by one point.
The last two long calls with strike price of $39 have a vega of 0.01.
In other words, the value of the 2 long calls will increase by 2 times $1 i.e. $2 if implied volatility increases by one point.
In total, the volatility of 3 long calls ($3.80) are almost offset by the volatility of 3 short calls ($4.29).
The combined position has a vega of -0.0049.
As a negative vega position, it will benefit from falling volatility. You can read more about implied volatility and vega in detail here
How Theta Impacts the Trade
The investor is long calls and short calls with different strike prices.
Long calls have negative time decay and short calls have positive time decay.
The initial long call with the lowest strike of $37.50 price will erode in value by $0.0533 per share i.e. $5 with each passing day.
The 3 short calls with strike of $38.50 will benefit by 3 times $0.0426 per share i.e. $13 for the 3 short calls with each passing day.
The last 2 long calls with strike of $39 will erode in value by 2 times $0.0341 per share i.e. $7 for the 2 long calls with each passing day.
The combined position has theta of -0.0063 of +$0.63 per day.
Ideally, the investor would like all options to expire worthless except the initial call with the lowest strike price.
Risks
Christmas tree with calls is a limited risk strategy with losses limited to the premium paid.
Additionally, this strategy should only be used if the investor is only slightly bullish.
A sharp decline in price below the initial strike price of $37.50 or a sharp increase in price above the highest strike of $39 will result in a loss.
Summary
A three-legged trade with six options sound complicated but once you are comfortable with these trades, they aren’t as complicated.
Both patience and execution are required to trade with Christmas trees and that only comes with experience.
Trade safe!
Disclaimer: The information above is for educational purposes only and should not be treated as investment advice. The strategy presented would not be suitable for investors who are not familiar with exchange traded options. Any readers interested in this strategy should do their own research and seek advice from a licensed financial adviser.










