

From our previous study, we know that calendar time spreads have positive vega.
Vega is one of the options Greeks use to inform us of how the trade will profit if implied volatility changes.
Contents
Introduction
When a trade has positive vega — we call this a long vega trade — it means that it should profit if implied volatility goes up, provided that volatility was the only thing that changed.
We say that it “should” because this is somewhat theoretical.
In reality, it may or may not, depending on many factors.
The profit is affected by the other Greeks, primarily Delta, which causes the profit and loss (P&L) to change as the price of the underlying moves.
Another Greek is Theta.
For calendars, theta is positive, meaning that a portion of the calendar value will increase daily (including non-trading days).
Another factor that affects the value of the calendar is how the implied volatility of the near-term option changes in relation to the far-term option.
This topic involves the amount of skew and contango, which we will not discuss today.
Regardless, some options traders would like to configure the amount of vega in their calendars, which is the topic of today’s discussion.
Narrow The Time Spread
The vega in the calendar is a function of the difference in vega between the long and short options.
If the trader wants to decrease the amount of vega in the calendar, the most readily available method is to decrease the time between the near and the far-term option.
When the two expirations are close to each other, their volatility differences usually will be less.
Hence, vega is less.
For example, here is a calendar with one week between the near-term short option and the far-term long option.
Date: April 16, 2024
Price: SPX @ 5062
Sell one contract May 3rd SPX 5060 put @ $69.25
Buy one contract May 10th SPX 5060 put @ $77.50
Debit: -$825
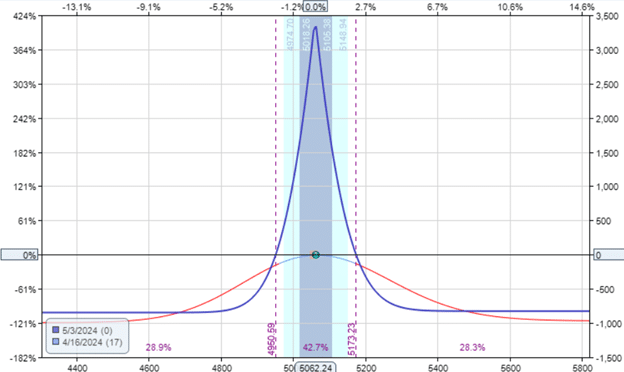
Delta: 0.15
Theta: 44.91
Vega: 81.91
Vega/Theta: 1.8
It has a vega of 82.
If we keep the near-term option the same but move the expiration of the far-term option closer to decrease the time gap between the expiration of the two options, we would have the following calendar:
Date: April 16, 2024
Price: SPX @ 5062
Sell one contract May 3rd SPX 5060 put @ $69.25
Buy one contract May 6 SPX 5060 put @ $71.20
Debit: -$195
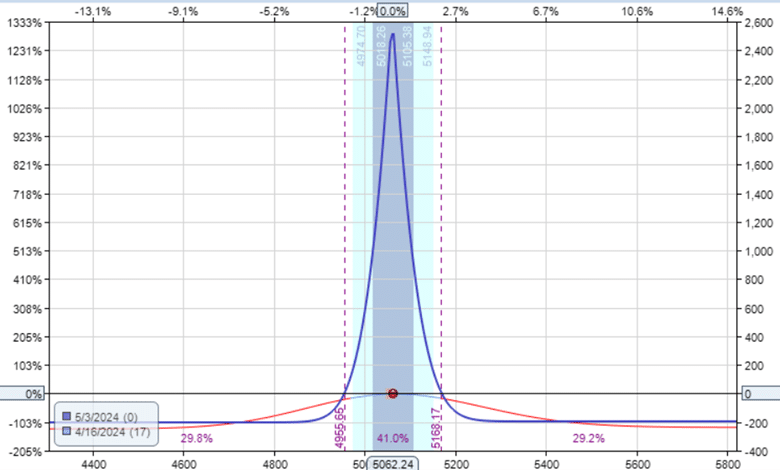
Delta: 0.01
Theta: 27.57
Vega: 36.85
Vega/Theta: 1.3
The vega has now decreased to 36.85.
But we have also lost theta.
This is true because this calendar is smaller and narrower (as you can see by comparing the width of the expiration break-even points).
However, the loss in theta is not proportional to the loss in vega (as can be noted by the difference in the Vega/Theta ratio).
In other words, we can have two such narrow calendars like this:
Date: April 16, 2024
Price: SPX @ 5062
Sell two contract May 3rd SPX 5060 put @ $69.25
Buy two contract May 6 SPX 5060 put @ $71.20
Debit: -$390
And the Greeks would be cumulative.
Delta: 0.02
Theta: 55.13
Vega: 73.70
Vega/Theta: 1.3
We have just as much and even more theta than the wide calendar.
And yet, our cumulative vega is still less than our wide calendar.
Reducing the DTE
Another way to decrease the vega/theta ratio is to reduce the days to expiration.
Here, we have a calendar with only ten days till expiration for the short option.
The long option is still three days further than the short option.
Date: April 16, 2024
Price: SPX @ 5062
Sell one contract April 26 SPX 5060 put @ $55.60
Buy one contract April 29 SPX 5060 put @ $58.55
Debit: -$295
The Greeks, for one contract, are:
Delta: 0.02
Theta: 55.15
Vega: 46.81
Those Greeks enable us to calculate the Vega/Theta ratio to be 0.84, lower than any of the example calendars shown thus far.
By reducing the number of days to expiration, we have decreased vega in relation to theta.
Suppose you think of vega as the volatility risk in a calendar.
And think of theta as the incoming generation engine of the calendar.
Then, a lower vega/theta ratio means a lower risk-to-reward ratio, which is another way of stating a better reward-to-risk ratio.
We are saying that by decreasing the time gap between expirations and by decreasing the days to expiration, we are increasing the reward-to-risk ratio of the calendar.
This calendar is even smaller and narrower:
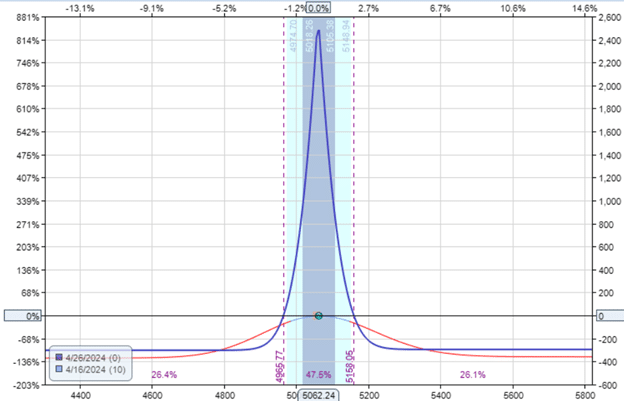
Reading off the graph, we see the reward-to-risk is about $2500 / $300 = 8.3.
The trader might want to increase the number of contracts to achieve the position size that they want.
However, the Vega/Theta ratio will not change as the number of contracts increases.
Conclusion
Calendars make money from the theta.
The vega represents volatility risk.
Traders who want to decrease their vega risk on their calendars without compromising on theta will want to decrease the vega in relation to the theta.
In other words, they want calendars with lower vega/theta ratios.
The vega/theta ratio can be reduced by decreasing the time difference between the expirations of the two options.
The shape of the calendar expiration graph will look more narrow.
The vega/theta ratio can also be reduced by decreasing the number of days till expiration (assuming we keep the time difference between the two options the same).
Tall skinny calendars may have a lower vega/theta ratio, which is good.
However, they also have a narrow range of profitability, which is not so good.
We hope you enjoyed this article on controlling the vega of calendar spreads.
If you have any questions, please send an email or leave a comment below.
Trade safe!
Disclaimer: The information above is for educational purposes only and should not be treated as investment advice. The strategy presented would not be suitable for investors who are not familiar with exchange traded options. Any readers interested in this strategy should do their own research and seek advice from a licensed financial adviser.










