

Time spreads are options strategies consisting of options that have different expiration dates.
When people hear time spread, the first thing that comes to mind is the calendar.
Contents
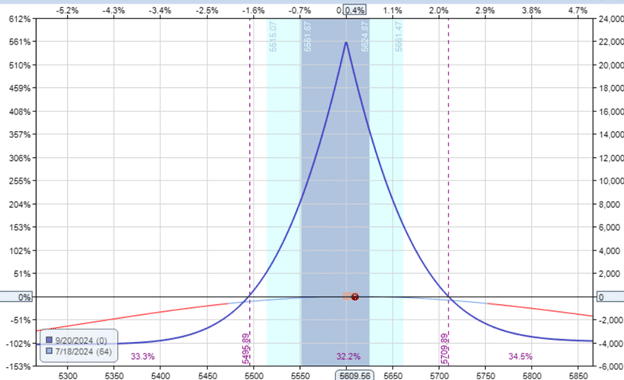
Let’s look at a calendar on the SPX index.
Date: July 18, 2024
Price: SPX @ 5610
Sell twenty Aug 2 SPX 5600 put @ $45.90
Buy twenty Aug 5 SPX 5600 put @ $47.70
Net Debit: -$3600
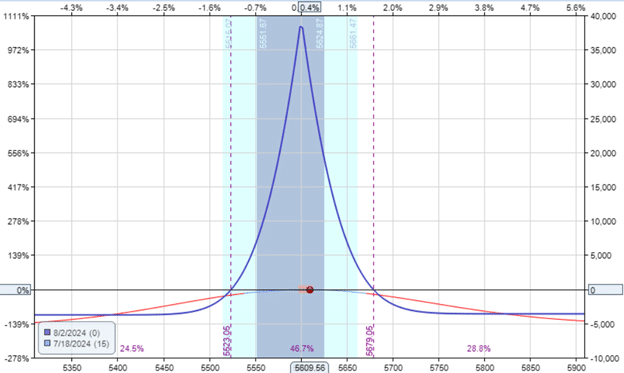
The first-order Greeks for this calendar are the Delta, theta, and Vega, as follows:
Delta: -1.4
Theta: 460
Vega: 864
They tell us how the P&L of the option position will change as the price, time, and volatility change.
Gamma is another options Greek.
It is a second-order Greek.
Second-order Greeks tell us the rate of change of the first-order Greeks.
In particular, Gamma tells us Delta’s rate of change with respect to the price of the underlying asset.
How will the Delta of our position change as the price moves up and down?
That is what Gamma tells us.
Our calendar has a Gamma of -0.3.
The negative value of Gamma means that as the price of SPX moves up, the Delta will decrease – meaning that if it is already negative, it will become even more negative.
Well, that’s not good for our calendar.
Looking at the risk graph, as the price of SPX goes up, our P&L will go down.
That’s the result of our negative Delta.
What’s even worse is that as SPX goes up, the Delta will become even more negative – making the position go against us even more.
That is the problem with having a negative Delta.
When a position goes against us, it makes the position go against us even more.
The larger the magnitude of Gamma, the more this effect is.
Therefore, if we have to have a negative Gamma (which is the case whenever we want positive theta in a premium selling strategy), we want the magnitude of that Gamma to be small.
What Does A Double Calendar Look Like?
Instead of a 20-lot calendar.
How about we split that into two calendars?
Ten contracts on the put side and ten contracts on the call side like this:
Sell ten Aug 2 SPX 5540 put @ $27.25
Buy ten Aug 5 SPX 5540 put @ $29.15
Sell ten Aug 2 SPX 5680 call @ $29.95
Buy ten Aug 5 SPX 5680 call @ $31.95
Net Debit: $3900
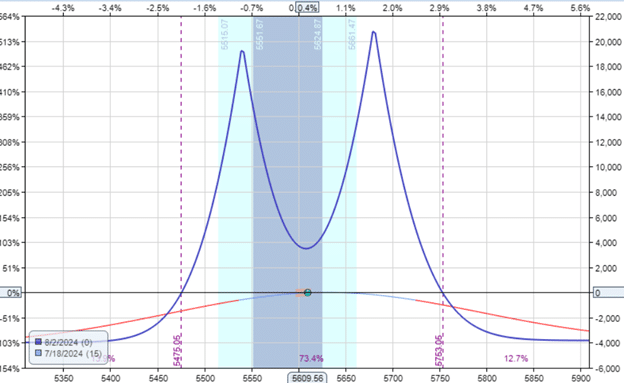
Delta: 2.95
Theta: 427
Vega: 847
Gamma: -0.28
The Gamma in this double-calendar is slightly lower at -0.28.
Double Diagonal
If we move the long strikes further away from the money, we get a double diagonal like this:
Buy three Aug 5 SPX 5520 put @ $24.65
Sell three Aug 2 SPX 5540 put @ $27.25
Sell three Aug 2 SPX 5680 call @ $29.95
Buy three Aug 5 SPX 5700 call @ $25.20
Net Debit: -$3795
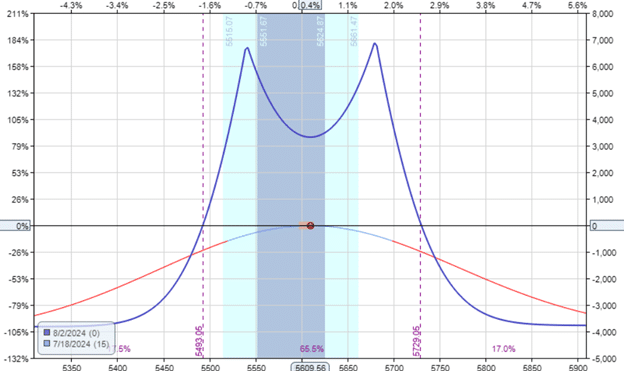
We’ve reduced the contract to three to get the capital invested to be somewhat similar to the previous examples.
The Greeks for the double diagonal are:
Delta: -0.12
Theta: 174
Vega: 81.2
Gamma: -0.14
Its Gamma is lower still at -0.14.
Another Way To Do A Double Diagonal
Another way to do the double diagonal is to have the long options closer to the money than the short options.
Sell four Aug 2 SPX 5550 put @ $29.75
Buy four Aug 5 SPX 5560 put @ $34.35
Buy four Aug 5 SPX 5660 call @ $39.95
Sell four Aug 2 SPX 5670 call @ $33.65
Net Debit: -$4360
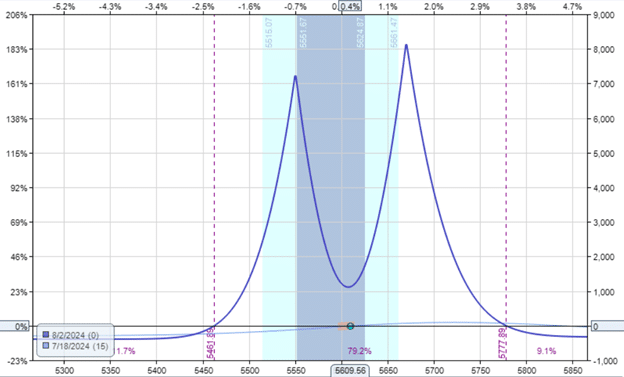
Even though the capital invested in this example at $4360 is larger than the previous examples, the Gamma is the lowest at -0.1
Delta: 1.61
Theta: 154
Vega: 431
Gamma: -0.10
Conclusion
These quick examples seem to show that double diagonals have lower Gamma and even more so if we move the long strikes closer to the money.
When you consider that long options have positive Gamma, it makes sense that option structures that give them more prominence will have less negative Gamma.
Does that mean that double diagonals always have smaller Gamma than calendars?
No.
By altering the expiration dates, I can easily make a calendar with a lower Gamma than the double diagonal. As in:
Sell seven Sep 20 SPX 5600 @ $89.45
Buy seven Spe 30 SPX 5600 @ $95.05
Net Debit: -$3920
Delta: 0.63
Theta: 45
Vega: 492
Gamma: -0.06
Does that mean that double diagonals are inherently better than calendars, and double calendars are better than single calendars?
No.
For every benefit you get, there is a disadvantage.
Scroll back through the article and look at the theta of each example.
When you get a smaller Gamma (advantage), you also get a smaller theta (disadvantage).
These quick examples show that Gamma and theta are intimately related.
We hope you enjoyed this article on the type of time spreads with the lowest Gamma.
If you have any questions, please send an email or leave a comment below.
Trade safe!
Disclaimer: The information above is for educational purposes only and should not be treated as investment advice. The strategy presented would not be suitable for investors who are not familiar with exchange traded options. Any readers interested in this strategy should do their own research and seek advice from a licensed financial adviser.










