Covered Calls and Compounding – The Eighth Wonder of the World

by Gavin in Blog, covered calls

October 11, 2014 • 3 comments

Albert Einstein once called compounding interest “the greatest mathematical discovery of all time”. I don’t know if I would go that far, but compounding is pretty amazing and has often been referred to as the eighth wonder of the world.

If we invested $10,000 in an account with simple interest of 5% p.a., we would earn $500 every year until we closed the account. At the end of five years, we would have made $2,500 in interest and have a total investment value of $12,500.

With  compound interest, we take that $500 earned each year and re-invest it each year. At the end of year one, we are now earning 5% interest on $10,500 and so on each year. At the end of year five we have $12,762.82.

The further out in time, the greater the benefits of compound interest as opposed to simple interest. At the end of thirty years, compound interest would earn $33,219.42 in interest as opposed to $15,000 from simple interest.

Interest in a bank account is one thing, but with a portfolio of covered calls, we would expect to earn a lot more than 5% p.a.  The earlier we learn about covered calls, the greater the benefits that are going to accrue to us.

With covered calls, it is possible to earn in the vicinity of 12-15% per year. Some people may achieve more if they take on more risk, and the results may be less during bear markets. But 12-15% is a good long run average for a conservative portfolio of covered calls.

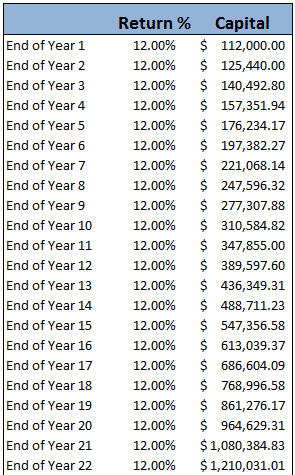
Taking a $100,000 portfolio, let’s take a look at how the benefits of covered calls can add up over the course of a lifetime. Let’s take a 30 year old, who has a 40 year investing horizon ahead of him.

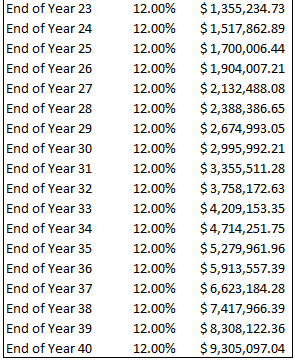
You would have to agree that turning $100,000 into $9,000,000 over a 40 year investing career is pretty impressive, but it is certainly possible.

This is one of the main premises that Warren Buffet preaches. He aims for consistent 10-20% returns per year over 40 odd years. Remember that the above table only considers the initial $100,000. Imagine how the returns would look if you added the 10-20% you should be saving from your salary each year. Just for fun, let’s take a look.

The following table assumes someone earning $100,000 per year and saving 20% of their salary. I’ve made the assumption that their salary will increase by 3% per year.

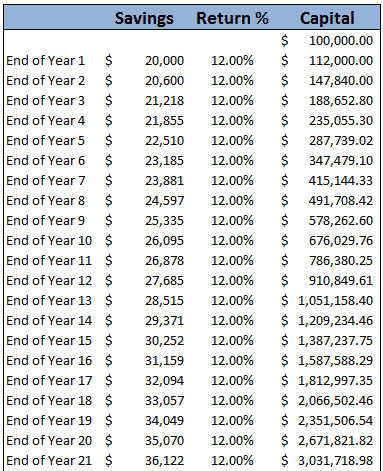
Ok so this is all theory and maybe it’s a bit unrealistic, so let’s try and make the results a bit more realistic.

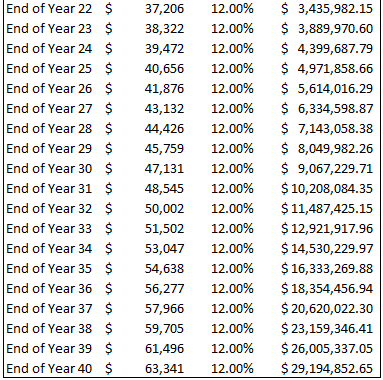
The stock market doesn’t always behave as expected, so let’s assume that you have the occasional negative year and throw in a bit more variation in the returns. Let’s also vary the savings rate a bit and assume no salary increases.

I’ve also assumed some years will have negative savings as people have kids, pay for college, cars, houses etc. I’ve thrown in some negative returns for good measure because they do happen after all!

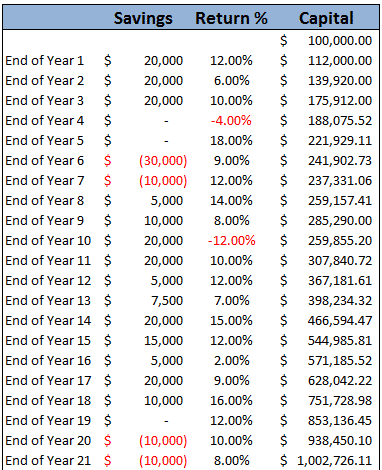
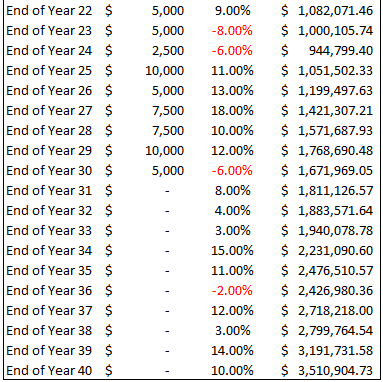
The numbers in the above table were entered completely randomly and we still turn $100,000 into $3.5 million over 40 years. The simple average return above works out at 7.93% so it is probably even a little bit conservative. Now that you know about covered calls and the power of compounding, all you need to do is come up with $100,000 and have a 40 year time frame. 😉